Skip to content

3.6.1 Periodic motion

3.6.1.1 Circular motion

Why does centripetal force exist

  • An object in a circular motion is constantly changing direction
  • Its velocity is changing hence it is accelerating
  • Acceleration requires a resultant force = centripetal force

Angular speed / velocity

  • \(\omega = \frac{d\theta}{dt} = \frac{2\pi}{T} = 2\pi f = \frac{v}{r}\)
  • Unit = rad \(s^{-1}\)
  • All points in a rotating object have the same angular velocity

Tangential / linear speed

  • \(v = r\omega\)
  • Unit = m \(s^{-1}\)

Centripetal acceleration

  • \(a = \frac{v^{2}}{r} = \omega^{2}r\)

Centripetal force

  • The force that acts towards the centre of the circular path i.e. acts perpendicular to the direction of motion
  • \(F = ma = \frac{mv^{2}}{r} = m\omega^{2}r\)

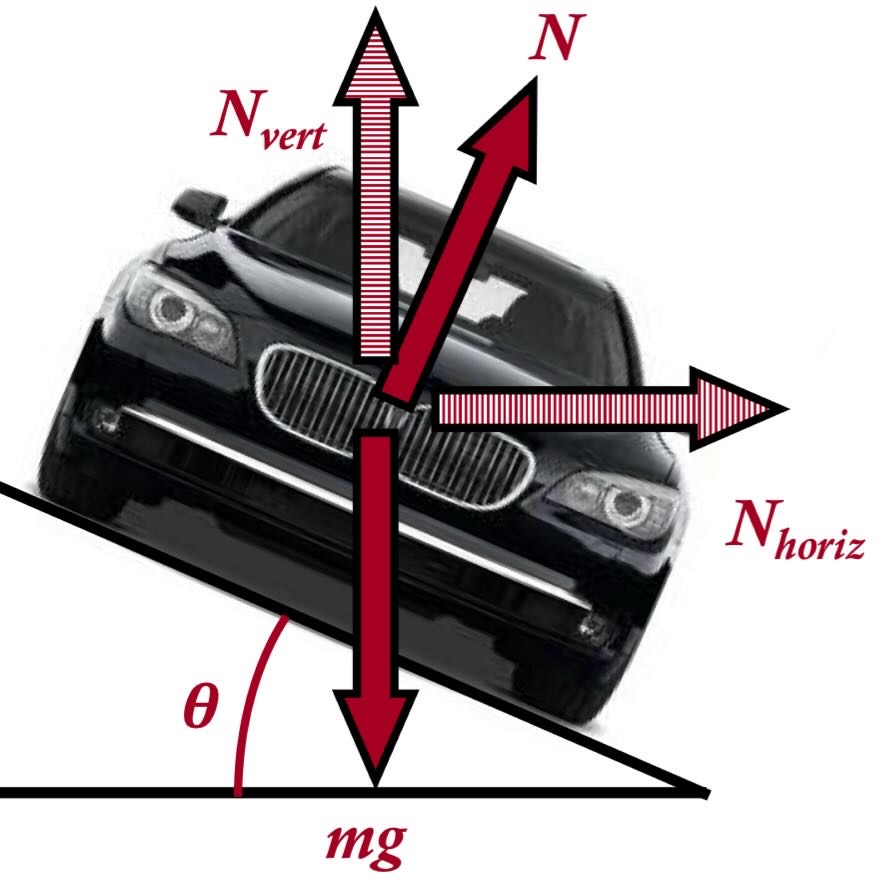
Banked tracks

  • Provide extra centripetal force via normal reaction force (horizontal component is towards the centre)
  • In horizontal track friction is the only source of centripetal force
  • Exported image|296x296

Roller coaster

  • Head pointing downwards: some centripetal force provided by the weight = less normal force
  • Head pointing upwards: more support force needed to counter the weight and provide centripetal force

3.6.1.2 Simple harmonic motion (SHM)

Simple harmonic motion

  • The acceleration of the object is proportional to the displacement in the opposite direction
  • Acceleration is directed towards the mean position
  • Defining equation for SHM: \(a = -\omega^{2} x\)

Period

  • Time for one complete oscillation

Amplitude

  • Maximum displacement from equilibrium position

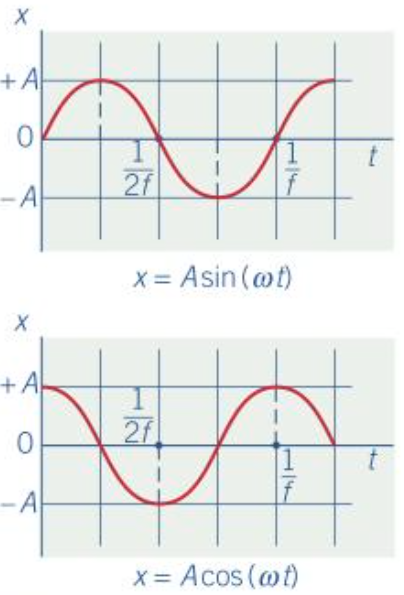
Mathematical solutions

  • Starting at 0 displacement
    • \(x = A \sin \omega t\)
    • \(v = A\omega \cos \omega t\)
    • \(a = -A\omega^{2} \sin \omega t\)
  • Starting at maximum displacement
    • \(x = A \cos \omega t\)
    • \(v = -A\omega \sin \omega t\)
    • \(a = -A\omega^{2} \cos \omega t\)
  • Velocity
    • \(v = \pm \omega \sqrt{A^{2} - x^{2}}\)
  • Maximum speed and acceleration
    • \(\text{Maximum speed} = \omega A\)
    • \(\text{Maximum acceleration} = \omega^{2} A\)
  • Exported image|225x390

Motion graphs for SHM

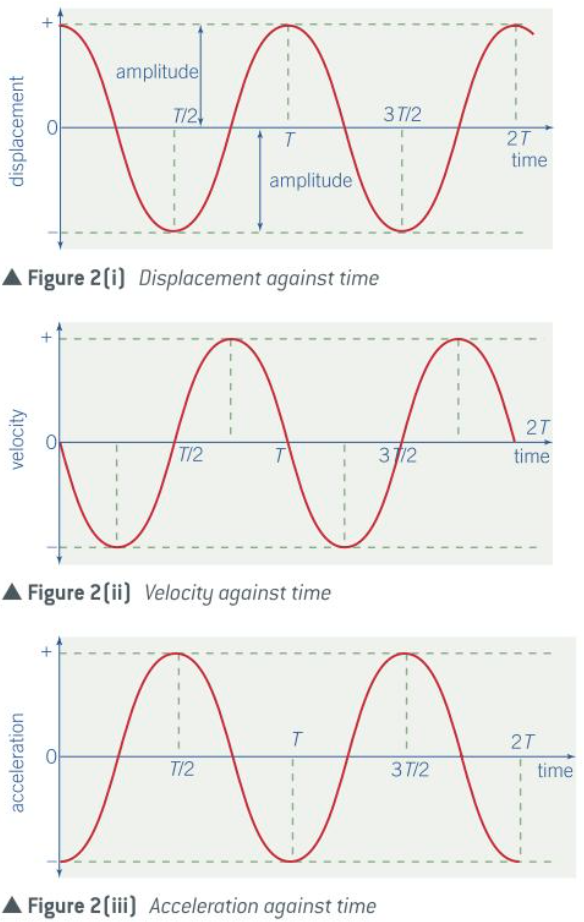
  • Exported image|350x553
  • Gradient of d-t graph = v-t graph
  • Gradient of v-t graph = a-t graph
  • Shifts to the left by \(\frac{\pi}{2}\) each time

3.6.1.3 Simple harmonic systems

Free oscillation

  • No energy lost during oscillations
  • Exported image|425x219

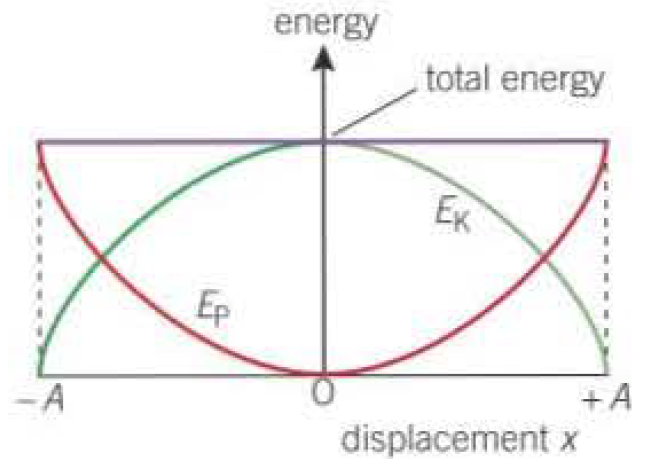
Energy changes

  • \(\text{Energy} \propto A^{2}\)
  • \(E = KE + PE\)
  • Kinetic energy
    • Minimum when \(x = \pm A\)
    • Maximum when \(x = 0\)
  • Potential energy
    • Minimum when \(x = 0\)
    • Maximum when \(x = \pm A\)
  • Total energy remains constant unless being forced / damped
  • Exported image|264x184

Mass-spring system

  • \(\omega = \sqrt{\frac{k}{m}}\)
  • \(T = \frac{2\pi}{\omega} = 2\pi \sqrt{\frac{m}{k}}\)
  • \(E_{k} = \frac{1}{2} kA^{2} - \frac{1}{2} kx^{2}\)

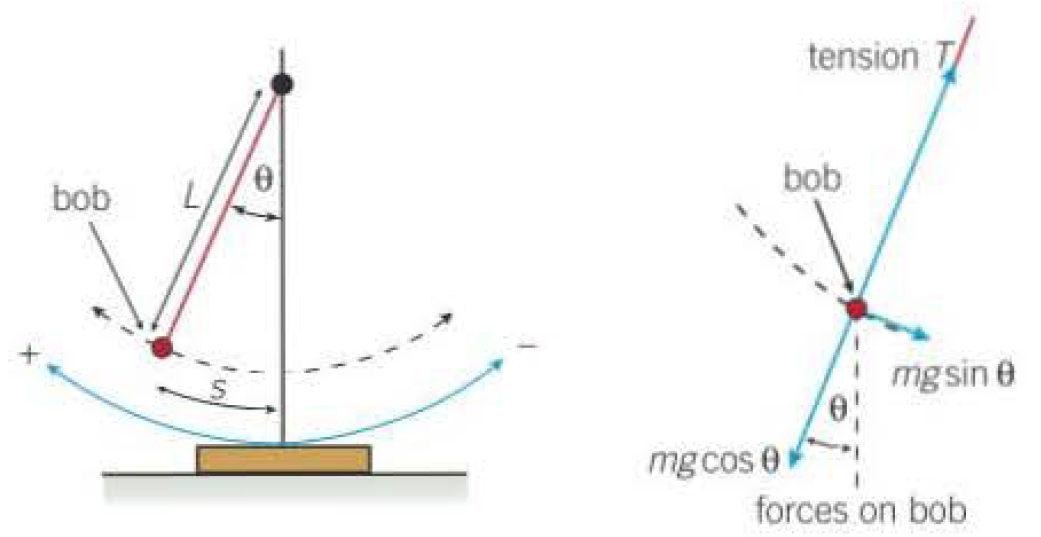
Simple pendulum

  • \(\omega = \sqrt{\frac{g}{l}}\)
  • \(T = \frac{2\pi}{\omega} = 2\pi \sqrt{\frac{l}{g}}\)
  • Only works when \(\theta\) does not exceed approx. 10° / amplitude is small

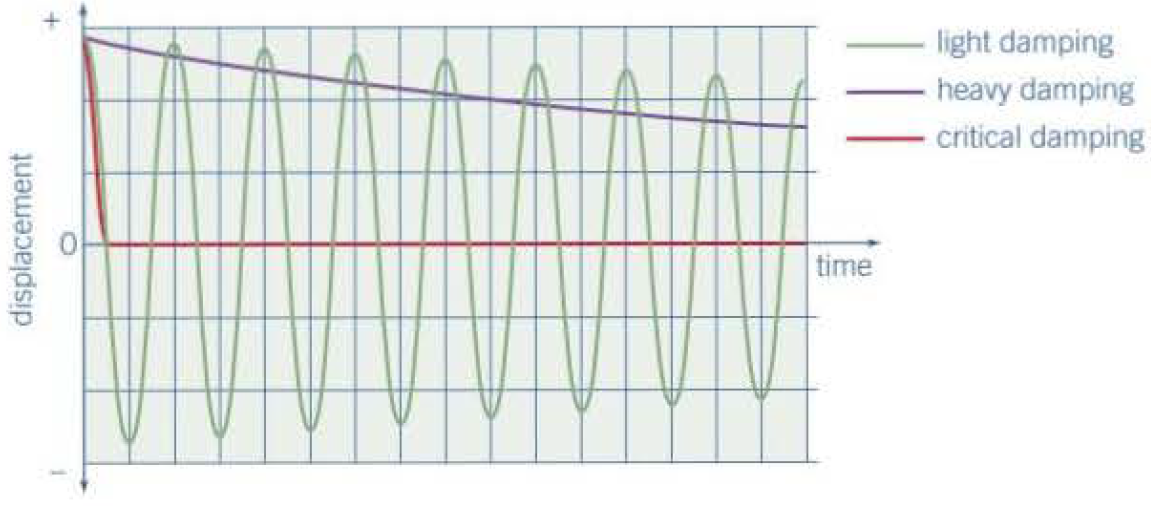
Damped oscillations

  • Oscillations that reduce in amplitude due to the presence of resistive forces
  • Lightly damped system
    • Amplitude decrease exponentially over time
    • Constant frequency
    • \(A = A_{0} e^{-Ct}\) (\(C\) is an arbitrary constant, depends on level of damping)
  • Critically damped system
    • System returns to equilibrium in the shortest possible time without oscillation
  • Heavily damped system
    • System returns to equilibrium more slowly than critical damping without oscillating
  • Exported image|522x229

3.6.1.4 Forced vibrations and resonance

Free vibrations

  • No damping \(\rightarrow\) the amplitude of the oscillations is constant
  • No periodic force acting on the system other than internal forces
  • No energy input

Forced vibrations

  • System made to oscillate by a periodic external force / energy source / another oscillator it is connected to
  • Oscillator is acted on by a periodic external force
  • Energy is given periodically by an external source
  • Made to oscillate at the frequency of another oscillator

Natural frequency (\(f_{0}\))

  • The frequency that an object oscillates at if it is displaced from its equilibrium position

Resonance

  • Applied frequency of the periodic force = the natural frequency of the system (state what is applied frequency / what produces it)
    • Phase difference between system and the periodic force = \(\frac{1}{2}\pi\)
    • Energy is transferred to the system more efficiently so the system gains max KE
  • The driving force continually supplies energy to the system
  • The amplitude of the oscillator increases
  • The amplitude would increase indefinitely if no resistive forces are present

Resonant frequency

  • The frequency with the maximum oscillating amplitude (the oscillating system in resonance)

Effect of damping on resonance frequency

  • Damping reduces the resonance frequency
  • When a system is damped, a resistive force is acting against the restoring force so the object travels slower \(\rightarrow\) lower resonance frequency

Amplitude-driving frequency graphs

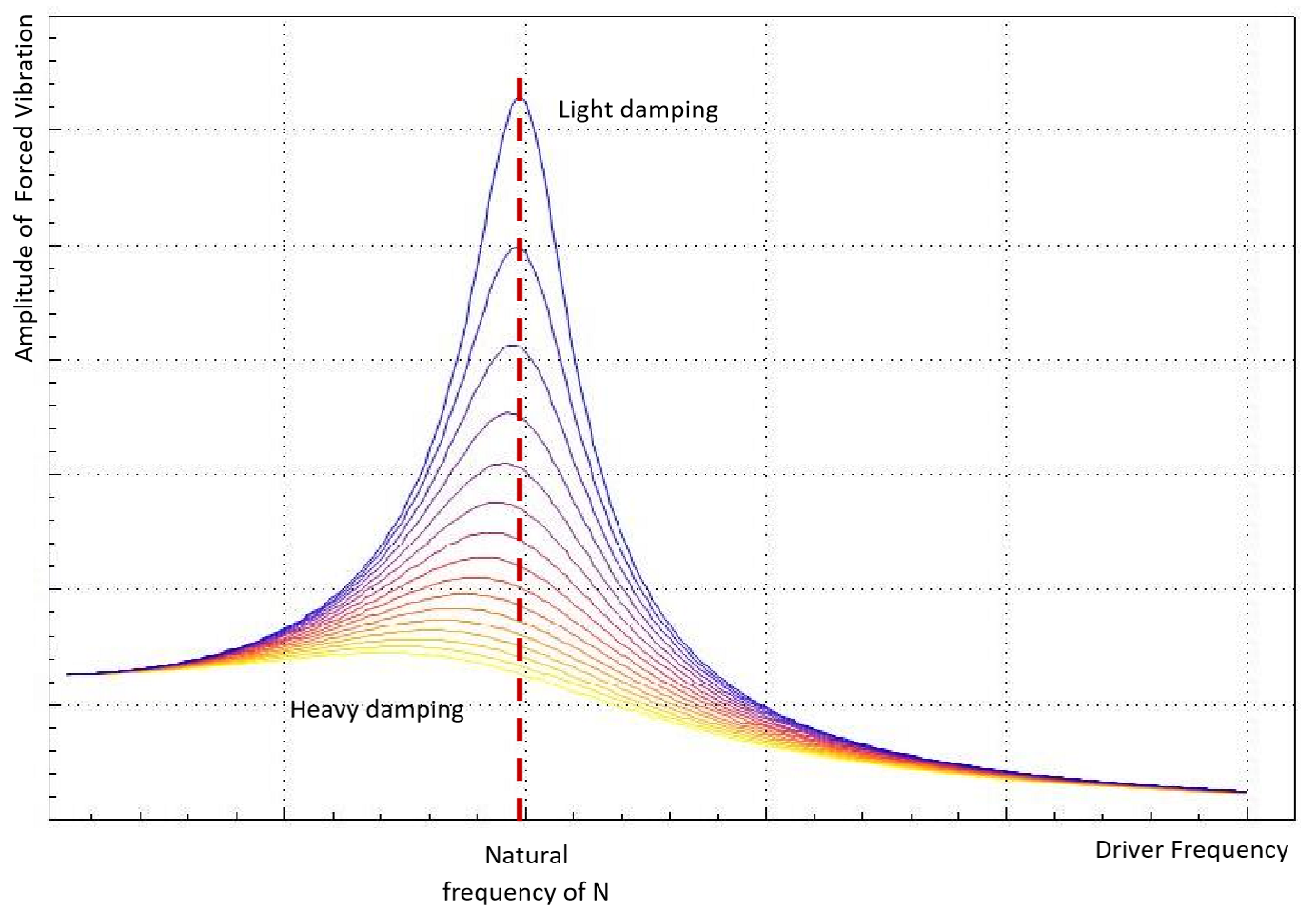
  • Exported image|578x401
  • More damping = smaller maximum amplitude at resonance
  • Less damping = sharpness of the peak amplitude of the curve increases, larger maximum amplitude
  • The closer the driving frequency is to the natural frequency the larger the amplitude

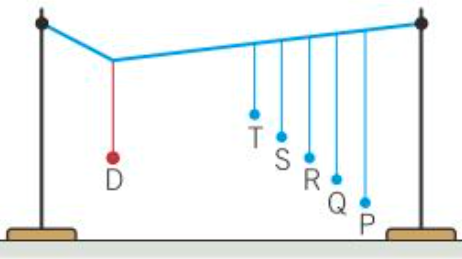
Barton's pendulums

  • The driver pendulum is displaced and released so that it oscillates in a plane perpendicular to the plane of the pendulums at rest
  • All pendulums swing at a very small amplitude except the one which has the same / similar length to the driver pendulum
    • \(T = 2\pi \sqrt{\frac{l}{g}}\)
    • Only that pendulum's frequency matches the natural frequency of the driver pendulum
    • \(\frac{\pi}{2}\) out of phase with the driver pendulum
    • Oscillates in resonance with the driver pendulum
  • Exported image|271x152