3.4.1 Force, energy and momentum

3.4.1.1 Scalars and vectors

Vector

• Any physical quantity that has a direction as well as a magnitude
• e.g. velocity, force / weight, acceleration, displacement

Scalar

• Any physical quantity that is not directional
• e.g. speed, mass, distance, temperature

Conditions for equilibrium

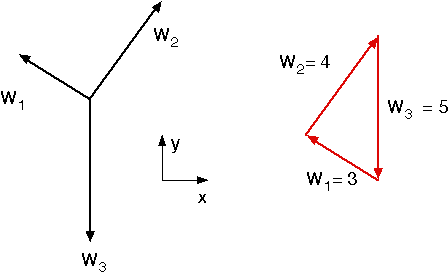
• For an object to be in equilibrium, the sum of all the forces acting on an it must be 0
• e.g. 3 forces form a closed triangle
  • 

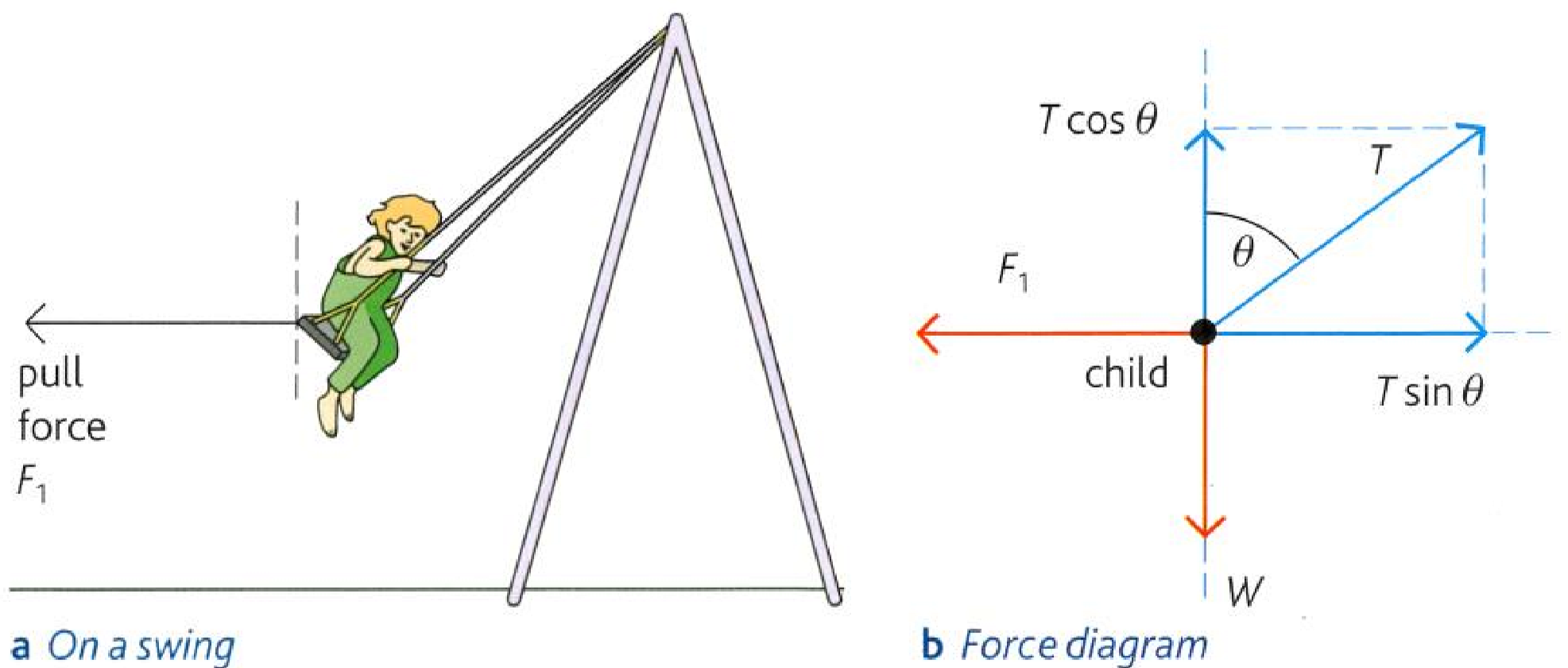
Explaining what forces balance each other

• e.g. child on swing
  • Pull force balances with the horizontal component of tension
  • Weight balances with the vertical component of tension
  • 

3.4.1.2 Moments

Moment formula

• \(\text{Moment of a force about a point} = \text{force} \times \text{perpendicular distance from the pivot point to the line of action of the force}\)

Couple

• A pair of equal and opposite parallel / coplanar forces acting on a body along different points
• Exerts a turning force on a body
• \(\text{Moment of couple} = \text{force} \times \text{perpendicular distance between the lines of action of the forces}\)

Principle of moments

• For an object in equilibrium, there is no resultant turning forces about any pivot

Centre of mass

• The point at which an object's mass / weight acts
• The point through which a single force on the body has no turning effect

Finding centre of mass

• Uniform regular solid
  • Centre of mass at the centre
• Non-regular card
  • Hang object (and plumb line) by first pivot
  • Draw first line vertically below pivot (by sketching a plumb line hang from the pivot)
  • Hang object (and the plumb line) by second pivot
  • Draw second line vertically below pivot
  • Intersection of lines is the centre of mass
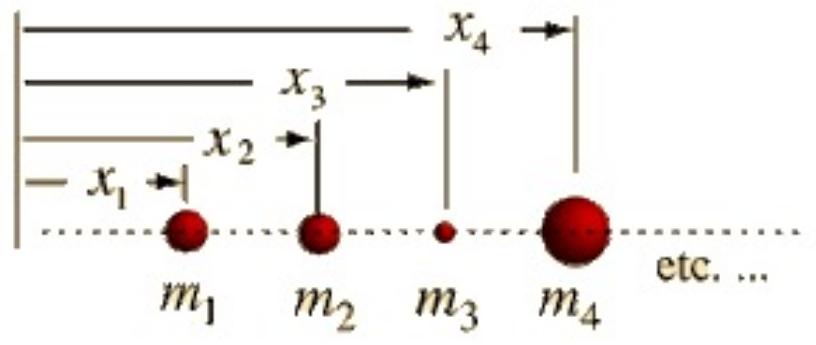
• Multiple mass on a rod
  • \(x_{cm} = \frac{\sum m_{i} x_{i}}{\sum m_{i}}\)
  • 

Equilibrium stability

• Stable
  • Object returns to its equilibrium position if displaced (a little)
  • Wide base, low centre of gravity
  • Tilted for a certain angle before centre of mass crosses the pivot point and topple
• Unstable
  • Object does not return to its equilibrium position if displaced
  • Topple immediately after being tilted
• Neutral
  • Stay in place when left alone
  • Stay in the new position when moved
  • The object's centre of mass is always exactly over the point which is its 'base'

Tilting / topping

• Tilting
  • An object resting on a surface is acted on by a force that raises it up on 1 side
  • For an object to tilt: \(Fd > \frac{Wb}{2}\) (\(b\) = width of base)
  • 
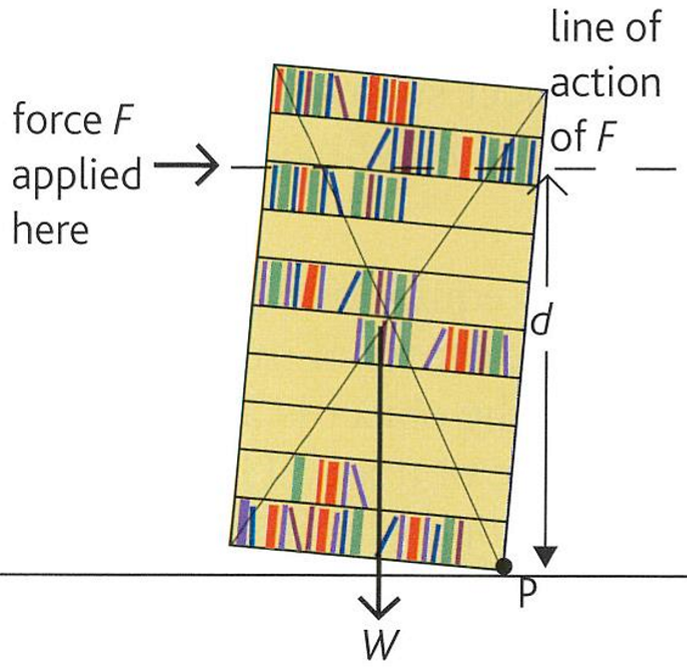
• Toppling
  • Tilted too far
  • Line of action of its weight passes beyond the pivot

Two support problems

• When an object is in equilibrium and supported by 2 points then the 2 supports add up to the weight of the object
• The support closer to the centre of mass provides more of the support force

On a slope

• The line of action of weight must lie inside the base of the object to prevent tilting
• 
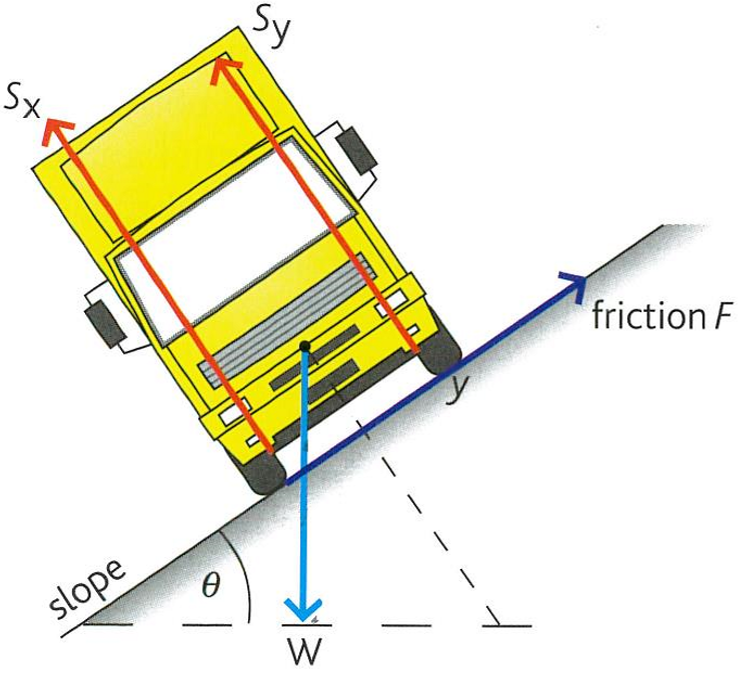
• \(S_{x} > S_{y}\) since \(x\) is lower than \(y\) (more moment is needed to be produced from \(x\) as it is closer to the centre of mass)

Conditions for equilibrium

• No resultant force
• No resultant moment / torque (the principle of moments must apply)

3.4.1.3 Motion along a straight line

Terms

Term	Definition
Speed	A scalar quantity describing how quickly an object is travelling
Displacement	The overall distance travelled from the starting position (includes a direction, vector quantity)
Velocity	Rate of change of displacement (\(= \frac{\Delta s}{\Delta t}\))
Instantaneous velocity	The velocity of an object at a specific point in time
Average velocity	The velocity of an object over a specified time frame
Acceleration	Rate of change of velocity (\(= \frac{\Delta v}{\Delta t}\))
Uniform acceleration	The acceleration of an object is constant

SUVAT equations

• For uniform acceleration
• \(v = u + at\)
• \(s = (\frac{u + v}{2}) t\)
• \(s = ut + \frac{1}{2} at^{2}\)
• \(s = vt - \frac{1}{2} (at)^{2}\)
• \(v^{2} = u^{2} + 2as\)

Motion graphs

	Displacement-time	Velocity-time	Acceleration-time
Gradient	Velocity	Acceleration	/
Area	/	(Change in) displacement	Change in velocity

Free fall

• \(u = 0\)
• \(a = g\)

Light gate

• \(\text{speed through the light gate} = \frac{\text{length of the object}}{\text{time for the light to be obscured}}\)

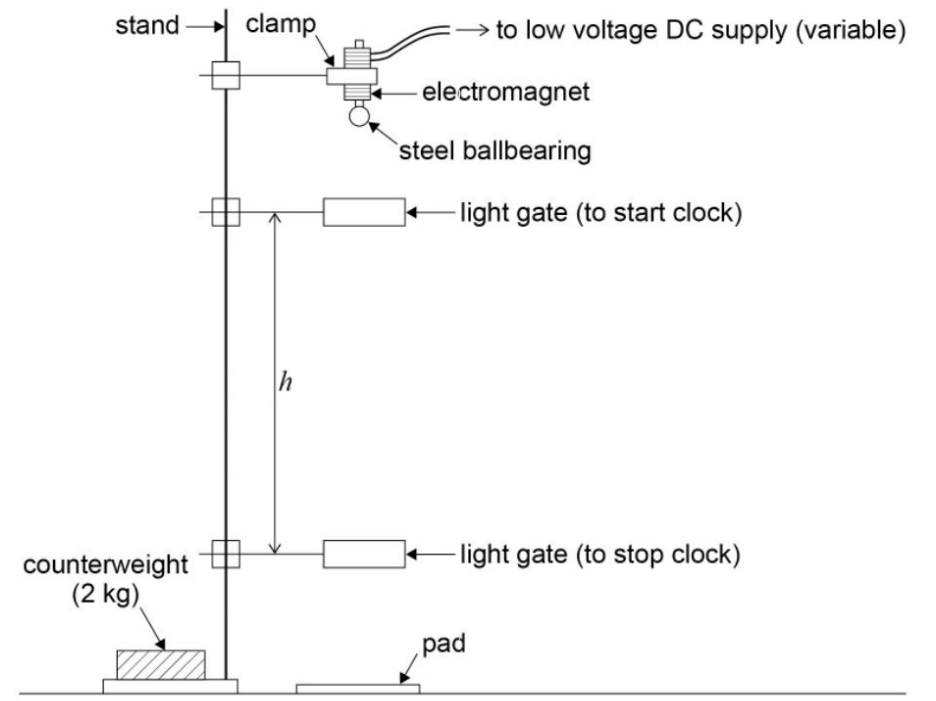
Required practical 3 - determining \(g\)

Equipment

• Stand
• Bosses and clamps
• Electromagnet
• Steel ball bearing
• Light gate
• Timer (connected to the light gate)
• Soft cushion pad

How to determine \(g\) by free fall

• Set up the apparatus as shown
  • 
• The position of the lower light gate should be adjusted such that the height \(h\) is 0.500m, measured using the metre rule
• Turn on the electromagnet and attach the ball bearing
• Reset the timer to zero and switch off the electromagnet
• Read and record the time \(t\) on the timer for the ball to pass through the 2 light dates
• Reduce \(h\) by 0.050m by moving the lower light gate upwards and repeat this, reducing h by 0.050m each time until \(h\) reaches 0.250m (at least 5-10 values of \(h\))
• Repeat the experiment twice more for each value of \(h\) and find and record the mean \(t\) for each \(h\)
• Plot a graph of \(\frac{2h}{t}\) against \(t\) and draw a line of best fit (\(\frac{2h}{t} = 2u + gt\))
• Gradient = \(g\), y-intercept = \(2u\)
  • (You might want to draw lines of maximum and minimum gradient and find the mean gradient)

Errors

• Systematic
  • Residue magnetism after the electromagnet is switched off may cause t to be recorded as longer than it should be
  • Air resistance reduces the value of \(g\) determined
• Random
  • Large uncertainty in \(h\) from using a metre rule with a precision of 1 mm
  • Parallax error from reading \(h\)
  • The ball may not fall accurately down the centre of each light gate (less time obscuring the light)
  • Random errors are reduced through repeating the experiment for each value of h at least 3-5 times and finding an average time, \(t\)

Safety

• The electromagnetic requires current
  • No water near it
  • Only switch on the current to the electromagnet once everything is set up to avoid electrocution
• A cushion or a soft surface must be used to catch the ball-bearing so it doesn’t roll off / damage the surface
• The tall clamp stand needs to be attached to a surface with a G clamp so it stays rigid

3.4.1.4 Projectile motion

Motion equations ignoring air resistance

• \(v_{x} = u \cos \theta\)
• \(x = ut \cos \theta\)
• \(v_{y} = u \sin \theta - gt\)
• \(y = ut \sin \theta - \frac{1}{2} gt^{2}\)

Range and maximum height formula (not required but useful)

• \(\text{Maximum height} = \frac{u^{2} (\sin \theta)^{2}}{2g}\)
• \(\text{Horizontal range} = \frac{u^{2} \sin 2\theta}{g}\)
• \(\text{Time to maximum height} = \frac{u \sin \theta}{g}\)
• \(\text{Time back to starting height} = \frac{2u \sin \theta}{g}\)

Friction

• A force which opposes the motion of an object
• AKA drag / air resistance
• Convert KE into other forms of energy such as heat and sound (work done on the surface / fluid)

Lift

• An upward force which acts on objects travelling in a fluid
• Caused by the object creating a change in the direction of the fluid flow
• Happens if the shape of the projectile causes the air to flow faster over the top of the object than underneath it
  • Pressure of air on the top surface < pressure of the air on the bottom surface
  • Produces a net upward force
• Acts perpendicular to the direction of fluid flow
• 

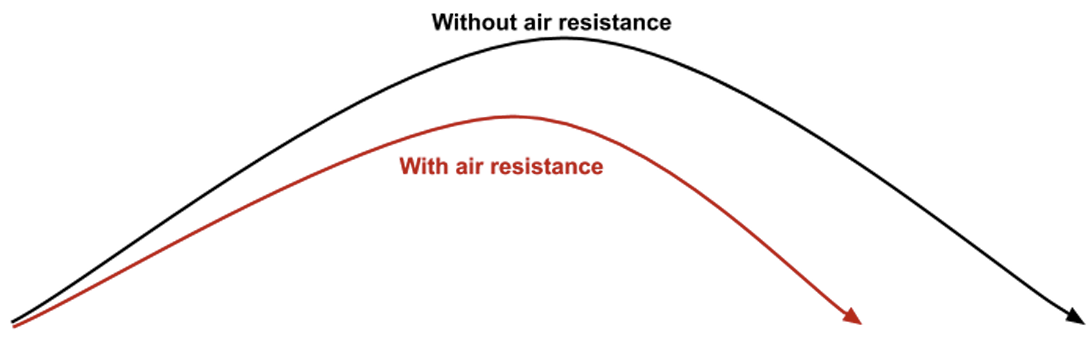
Effect of air resistance (friction)

• Air resistance / drag force acts in the opposite direction of motion of the projectile
• Increases as the projectile's speed increases
• Has both horizontal and vertical components
• Reduces both the horizontal speed of the projectile and its range
• Reduces the maximum height of the projectile if its initial direction is above the horizontal and makes its descent steeper than its ascent
• 

Terminal velocity

• Occurs where the frictional forces acting on an object and the driving forces are equal
• No resultant force \(\rightarrow\) no acceleration \(\rightarrow\) travels at constant speed / velocity

Terminal velocity for objects falling

• Start initially with free fall (uniform acceleration) briefly
  • The only force acting on the object is weight
  • (Other forces are very small and negligible)
• Speed still increases but acceleration decreases
  • Air resistance increase because speed increase
  • Resultant force gets smaller
• Eventually the object falls in uniform velocity (reached terminal velocity)
  • Weight balanced exactly by resistive force upwards
  • Resultant force = 0 so there is no acceleration
  • Air resistance is not increasing anymore because speed is not increasing
  • Potential energy of the object is transferred to the internal energy of the fluid by drag forces
• Effect of parachute
  • Increase air resistance due to larger area perpendicular to direction of travelling
  • Resultant force upwards so deceleration
  • Air resistance falls as speed falls
  • Decelerates until air resistance get as big as speed so the object falls at uniform speed again
• Graph
  • Gradient should start with gradient 9.81 \(ms^{-2}\) not bigger than 9.81 \(ms^{-2}\)
  • 
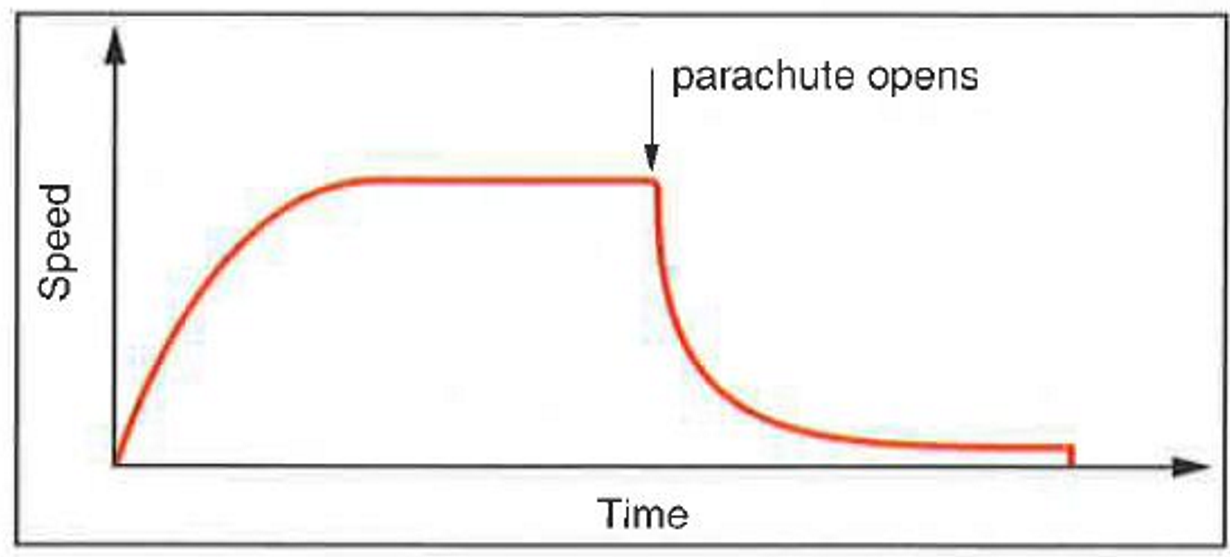
• (Same to other situations moving through a fluid - resistance increase until the maximum speed is reached)

Factors affecting terminal velocity

• Higher mass \(\rightarrow\) higher acceleration \(\rightarrow\) higher terminal velocity
• Higher volume / CSA \(\rightarrow\) more air resistance \(\rightarrow\) less acceleration \(\rightarrow\)' lower terminal velocity

3.4.1.5 Newton’s laws of motion

Newton's 1st law of motion

• If no resultant external force are acting on a body, it will
  • If at rest, remain at rest
  • If moving, keep moving at constant speed in a straight line

Newton's 2nd law of motion

• The acceleration of an object is proportional to the resultant force experienced by the object
• Acceleration is in the same direction as the resultant force
• \(\text{resultant force} = \text{mass} \times \text{acceleration}\)
• \(F = ma\)

Newton's 3rd law of motion

• When two objects interact, they exert equal and opposite forces on each other

3.4.1.6 Momentum

Momentum calculation

• \(\text{Momentum} = \text{mass} \times \text{velocity}\)
• \(p = mv\)

The principle of conservation of momentum

• Momentum is always conserved for a system of interacting objects provided that no external resultant force acts on the system
• Total final momentum = total initial momentum

Types of collisions

• Elastic
  • There is no loss of kinetic energy during the collision
  • Both momentum and KE are conserved
  • \(m_{1} u_{1} + m_{2} u_{2} = m_{1} v_{1} + m_{2} v_{2}\)
• Inelastic: only momentum is conserved, some KE is lost
  • Stick together: \(m_{1} u_{1} + m_{2} u_{2} = (m_{1} + m_{2}) v_{1 + 2}\)
  • Colliding objects have less KE after the collision than before the collision

Explosion

• \(m_{1} v_{1} + m_{2} v_{2} = 0\)
• KE of the objects has increased

Newton's 2nd law of motion using momentum

• The rate of change of momentum of an object is equal to the resultant force on it
• \(F = \frac{\Delta (mv)}{\Delta t}\)

Impulse

• The change in momentum
• \(\text{Impulse} = F \Delta t = \Delta (mv)\)

Force-time graph

• Area = \(F \Delta t\) = change in momentum

Stopping distances

• \(\text{Thinking distance } s_{1} = \text{speed} \times \text{reaction time} = ut_{0}\)
• \(\text{Braking distance } s_{2} = \frac{u^{2}}{2a}\)
• \(\text{Stopping distance} = s_{1} + s_{2} = ut_{0} + \frac{u^{2}}{2a}\)

Contact and impact time

• \(\text{impact time} = \frac{2s}{u + v} = \frac{2 \times \text{distance moved by cars}}{\text{initial velocity} + \text{final velocity (of the same car)}}\)
• \(a = \frac{v - u}{t}\)
• \(F = ma = \frac{mv - mu}{t}\)
• (These calculations only need to be applied onto one car)

Why airbags / seatbelts / etc. work

• With no seat belt / airbag / etc. the person would not start to change their momentum until they hit the dashboard or windscreen
• The person comes to stop quickly (short impact time)
  • Large change of momentum in a short time = large resultant force = large injury (\(F = \frac{\Delta (mv)}{t}\))
• With the seatbelt / airbag / etc. they will have a longer impact time (comes to stop more slowly)
  • They will experience a smaller resultant force and so less injury

3.4.1.7 Work, energy and power

Work

• \(\text{Work done} = \text{force} \times \text{distance moved in the direction of the force}\)
• Unit = joules (J)
• \(W = Fs \cos \theta = \text{force} \times \text{displacement} \times \text{angle between force and direction of motion}\)

Force-displacement graphs

• Area under line = work done

Power

• Rate of doing work = rate of energy transfer
• \(P = \frac{\Delta E}{\Delta t} = \frac{\Delta W}{\Delta t} = Fv \cos \theta = \text{driving force} \times \text{velocity} \times \cos \theta\)

Efficiency

• \(\text{Efficiency} = \frac{\text{Useful work done}}{\text{Total energy input}} = \frac{\text{Useful energy output}}{\text{Total energy input}} = \frac{\text{Useful power output}}{\text{Total power input}}\)
• Can be expressed as a percentage

3.4.1.8 Conservation of energy

Principle of conservation of energy

• Energy cannot be created or destroyed but transferred from one store to another

Kinetic energy

• \(E_{k} = \frac{1}{2} mv^{2}\)

(Gravitational) potential energy

• \(E_{p} = mg \Delta h\)