3.3.2 Refraction, diffraction and interference

3.3.2.1 Interference

Coherence

• Waves with a constant phase difference and the same frequency and wavelength

Monochromatic

• Light waves with a single wavelength only

Lasers

• Coherent and monochromatic
• Usually used as sources of light in diffraction experiments as they form clear interference patterns

Path difference

• The difference in the distance travelled by two waves from their sources to where they meet

Interference of monochromatic light

• Path difference = \(n\lambda\) \(\rightarrow\) constructive interference, gives maximum intensity / reinforcement
• Path difference = \((n + \frac{1}{2}) \lambda\) \(\rightarrow\) destructive interference, gives 0 intensity / cancellation

Interference of longitudinal waves (sound waves)

• Constructive interference / reinforcement
  • Compression + compression / rarefaction + rarefaction \(\rightarrow\) greater volume
• Destructive interference / cancellation
  • Compression + rarefaction \(\rightarrow\) 0 volume, used for noise cancellation

Young’s double slit experiment

• Condition for light source
  • Monochromatic light source \(\rightarrow\) use colour filter
  • Coherent \(\rightarrow\) single silt between light source and double silt
    • Both slits will be illuminated from the same source so they receive light of the same wavelength
    • Paths to both slits are of constant length giving constant phase difference (normally in phase)
  • Laser is both monochromatic + coherent so no colour filter / single slit needed
• Procedure
  • Shine a coherent light source through 2 slits about the same size as the wavelength of laser light so the light diffracts / use 2 coherent sources
  • Each slit acts as a coherent point source making a pattern of light and dark fringes
  • Light fringes are formed where the light from both slits meet in phase and interferes constructively (path difference = \(n\lambda\))
  • Dark fringes are formed where the light from both slits meets completely out of phase and interferes destructively (path difference = \((n + \frac{1}{2}) \lambda\))
  • 
  • 

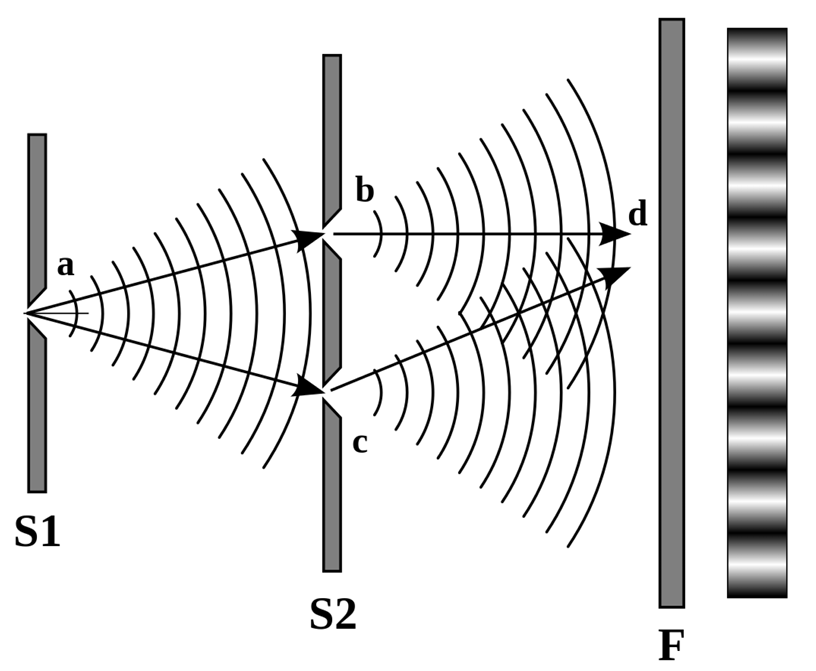
(Bright) Fringe spacing

• \(w = \frac{\lambda D}{s} = \frac{\text{wavelength} \times \text{distance between slit and screen}}{\text{slit spacing}}\)

Fringe spacing proof

• 
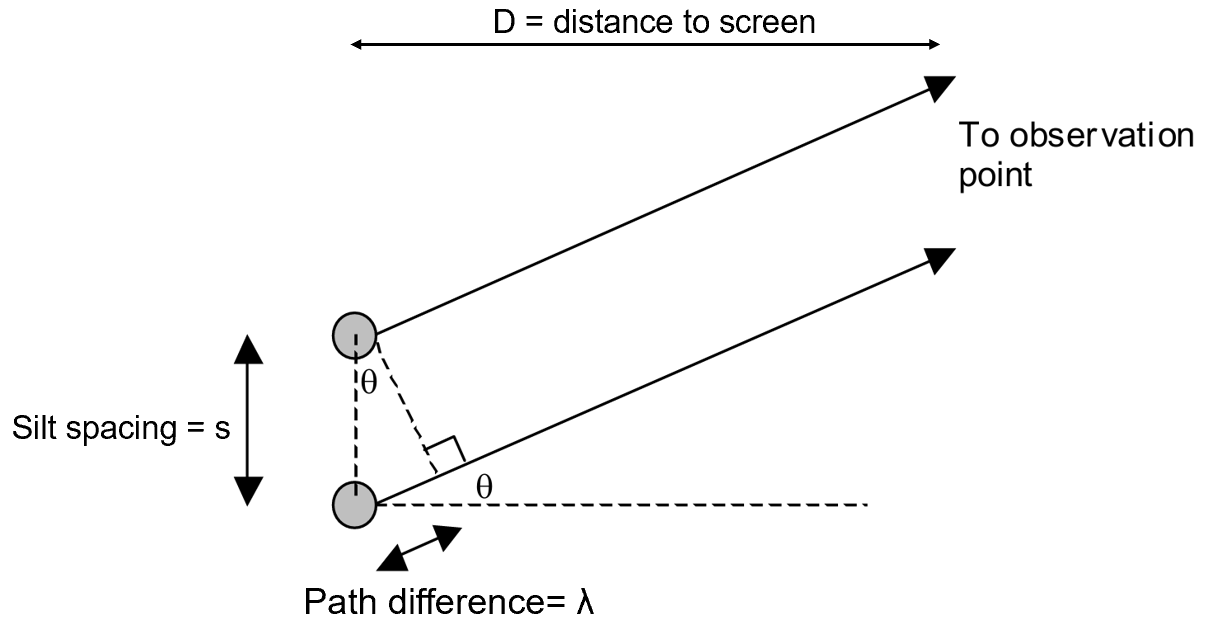
• \(\sin \theta = \frac{\lambda}{s}\)
• \(\tan \theta = \frac{w}{D}\)
• When \(\theta\) is small: \(\sin \theta \approx \tan \theta \approx \theta\) so \(\frac{\lambda}{s} = \frac{w}{D}\)
• Hence \(w = \frac{\lambda D}{s}\)

Significance of Young's double slit experiment

• Proved the wave nature of light since diffraction and interference are wave properties
• Proved that EM radiation must act as a wave
• Disproved the theories that light is formed of tiny particles
• Knowledge and understanding of any scientific concept changes over time in accordance to the experimental evidence gathered by the scientific community

Interference pattern with white light

• Wider maxima
• Less intense diffraction pattern with a central white fringe (all colours are present)
• Alternating bright fringes which are spectra, violet is the closest to the central maximum and red is the furthest

Safety precautions with lasers

• Do not look directly at a laser beam even when it is reflected
• Wear laser safety goggles
• Don’t shine the laser at reflective surfaces
• Display a warning sign
• Never shine the laser at a person

Required practical 2

Determining slit separation for double slit

• Illuminate a double slit with a red laser of known wavelength, \(\lambda\)
• Project the interference pattern onto a white screen a distance, \(D\), away from the slits
  • Measure \(D\) with a tape measure
• The fringe spacing, \(w\), can be measured by measuring across several visible fringes
  • Measure \(w\) using a meter rule
  • Find the mean fringe spacing
• Use the double slit formula, \(w = \frac{\lambda D}{s}\) and the measurements to determine the slit separation, \(s\).

Finding average grating spacing

• Illuminate a diffraction grating with a known grating spacing with a red laser of known wavelength, \(\lambda\)
• Project the diffraction pattern onto a white screen at a distance \(D\) away from the grating.
  • Measure \(D\) with a tape measure
• Measure the angles of diffraction, \(\theta_{n}\) for multiple diffraction maxima
  • Measure distance from centre + use trigonometry
• Plot a graph of \(\sin \theta_{n}\) against \(n\)
  • \(\text{gradient} = \frac{\lambda}{d}\)
  • Use the gradient to determine the average grating spacing \(d\) and hence the average number of lines per mm, \(\frac{1}{d}\)
• 

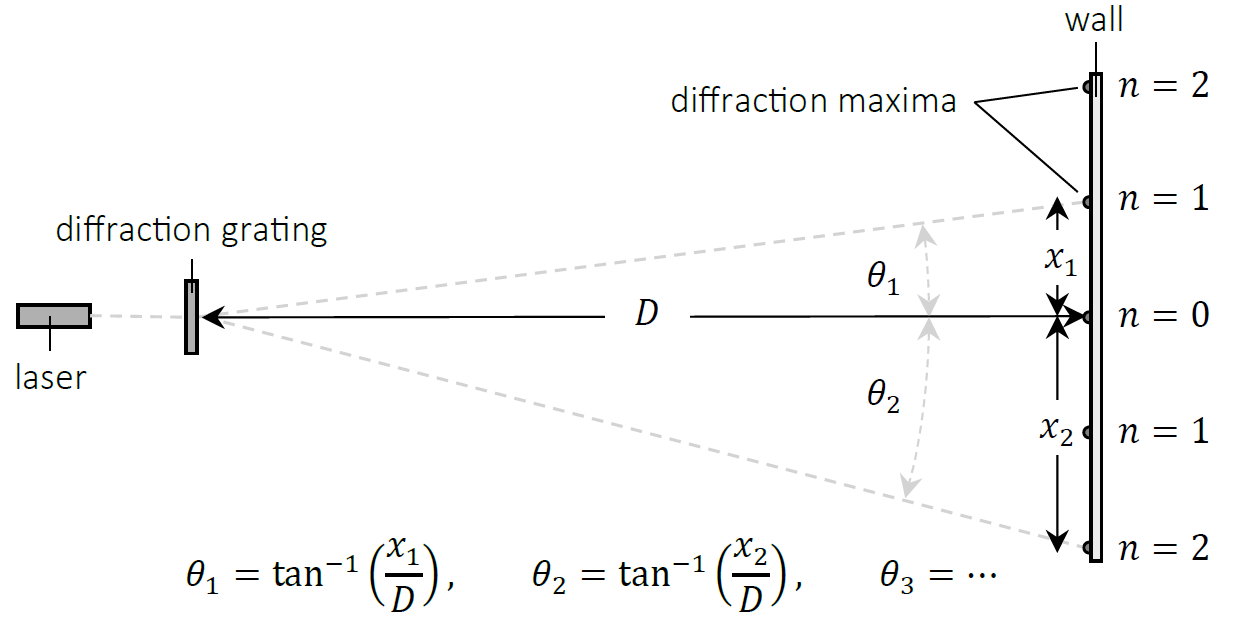
Finding wavelength of light

• Use a diffraction grating with a known average grating spacing and use the gradient to find the wavelength instead, otherwise same as above

3.3.2.2 Diffraction

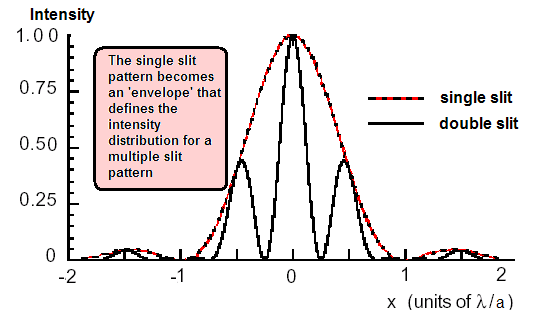
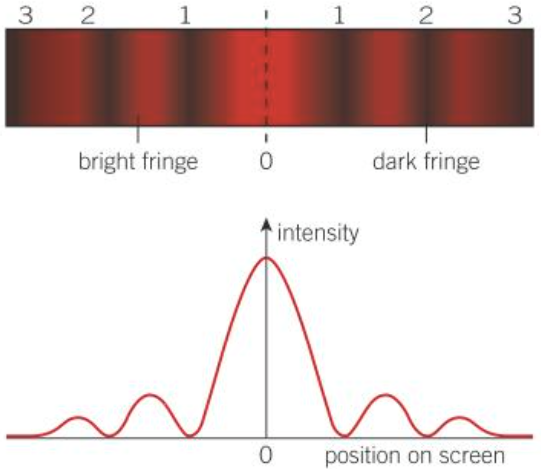
Single silt diffraction with monochromatic light

• Central maximum with highest intensity
• Decreasing intensity fringes on both sides, equally spaced
• Central fringe is twice the width of other fringes
• 

Single silt diffraction with white (non-monochromatic) light

• White central maximum
• Distinct fringes shown with subsidiary maxima
• Fringes on both sides show as spectrums
• Red furthest, violet closest to the centre in subsidiary maxima
• 

Effect of using narrower slit / longer wavelength

• Waves are more diffracted
• Wider spacing
• Lower intensity of fringes as the energy is spread over a larger area

Fringe spacing for single slit diffraction

• \(w = \frac{\lambda \times \text{distance from slit to screen}}{\text{slit width}} = \frac{\lambda D}{a}\)

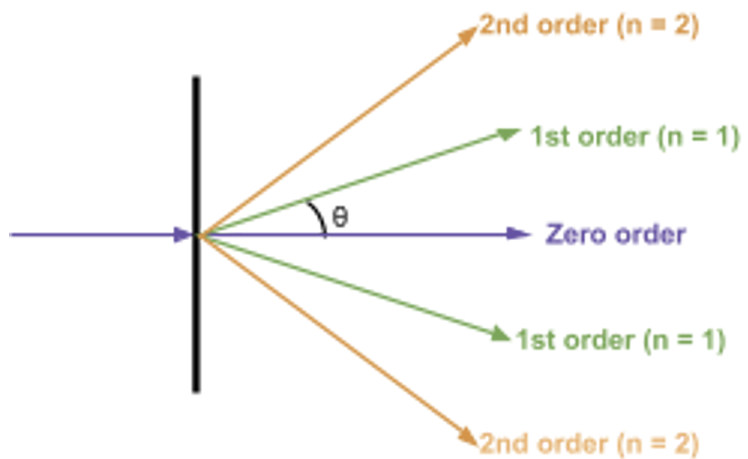
Diffraction grating explanation

• A slide containing many equally spaced slits very close together
• Light passing through each slit is diffracted
• Light from different slits superpose
• When the path difference between adjacent slits is a whole number of wavelengths the light waves arrive in phase and constructive interference occurs
• \(\text{Distances from the centre where maxima occur} = d \sin \theta = n\lambda\) (\(d\) = distance between slits)
  • Angle of diffraction between each transmitted beam and the central beam increases if light of a longer wavelength or a grating with closer slits is used
• 

Comparison to double slit

• Much sharper and brighter image when monochromatic light is passed through

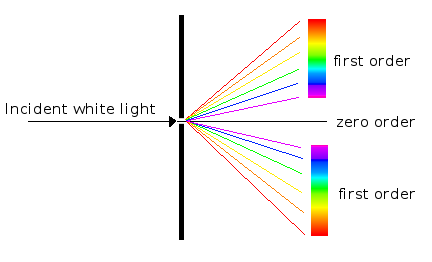
White light incident

• Spectrum is seen when white light is used
• Different colours of light have different maxima positions
• Line absorption spectra and line emission spectra can determine the elements in a substance (see photoelectric effect)

Maximum number of orders visible

• Use \(\sin \theta \le 1\)
• \(n_{max} = \lfloor \frac{d}{\lambda} \rfloor\)

Measuring wavelength of light

• Diffraction patterns are measured using a spectrometer
  • Angles measured accurate to 1 arc minute (\(\frac{1}{60}^\circ\))
• It can be used to study light from any source and measure wavelengths very accurately
• Angle measured using a known wavelength \(\rightarrow\) grating spacing calculated
• Grating can then be used to measure the wavelength of any light

Applications of diffraction grating

• Diffraction gratings can be used to observe and measure spectral lines
• Line emission spectra can be used to identify elements in the vapour gas of the vapour lamp (similar to line absorption spectra)

3.3.2.3 Refraction at a plane surface

Refraction

• Change of direction and wavelength when a wave crosses a boundary and its speed changes

Refractive index of a substance

• \(n = \frac{c}{c_{s}} = \frac{\sin i}{\sin r}\)
• Refractive index of air \(\approx 1\)
• Higher refractive index = light travels slower in the substance

Refractive index of different colours

• Longer wavelength = smaller refractive index = travels faster
• Red has the smallest refractive index as it has the longest wavelength
• Violet has the largest refractive index as it has the shortest wavelength

Snell's law

• \(n_{1} \sin \theta_{1} = n_{2} \sin \theta_{2}\)

Total internal reflection (TIR)

• For ray going from more dense to less dense substance & the angle of incidence exceeds the critical angle
• No refracted light wave since the angle of refraction > 90° so all the light is reflected

Critical angle

• The angle of incidence at which the angle of refraction is 90°
• \(\sin \theta_{c} = \frac{n_{2}}{n_{1}} \quad (n_{2} < n_{1})\)

Pulse broadening

• The length of a pulse is widened so it may overlap with the next pulse
• Distorts the information in the final pulse

Pulse absorption

• Energy is absorbed by the fibre
• Amplitude is reduced so information can be lost

Solution to pulse absorption

• Use more transparent core
• Use pulse repeaters to regenerate the pulse before significant pulse broadening has taken place

Material / spectral dispersion

• Happens if white light is used instead of monochromatic light
• Different wavelengths have different speeds due to different refractive indices within the core
  • Red light has the longest wavelength \(\rightarrow\) lowest refractive index, fastest
  • Violet light has the shortest wavelength \(\rightarrow\) highest refractive index, slowest
• Causes pulse broadening

Solution to material dispersion

• Use monochromatic light
• Use of shorter repeaters so that the pulse is reformed before significant pulse broadening has taken place

Modal / multipath dispersion

• Light waves entered at different angles of incidence so they are spread out
• They travel different distances as they take different paths and arrive at the other end at different times
• Causes pulse broadening

Solution to modal dispersion

• Use monomode fibre / narrower core
• Use a cladding with its refractive index as close to the core as possible (larger critical angle \(\rightarrow\) less TIR)

Optical fibre structure

• Core
  • The transmission medium for EM waves to progress
• Cladding
  • Protects the outer surface of the core from scratching which could lead to light leaving the core
  • Ensure that no light leaves the core
  • RI of cladding < RI of core
  • Maintains quality/reduces pulse broadening
  • Prevent crossover of signal to other fibres

Refractive index of cladding

• Similar RI between cladding and core
  • Larger critical angle \(\rightarrow\) less TIR \(\rightarrow\) less modal dispersion
• RI of cladding much smaller than core
  • Smaller critical angle (greater acceptance angle) \(\rightarrow\) less light escape \(\rightarrow\) more light collected

Types of optical fibre

• Step index fibre
  • The refractive index of each component increases moving from the outside to the centre of the fibre
  • The refractive index within each component is uniform
• Graded index fibre
  • Has a core that has a gradually increasing refractive index from outside to centre

Applications of optical fibres

• Endoscopes
• Transmission of data for communications

Producing coherent image

• An incoherent bundle cannot be used to form an image because the ends of the individual fibres are arranged randomly so the image is incorrect
• In a coherent bundle, the fibres have the same spatial position at each end of the bundle.
• The light emitted from the end of the bundle is an exact copy of the incident light and a single image can be reproduced and analysed
• Coherent bundles are expensive to manufacture so incoherent bundles are used for illumination

Advantages of optical fibres

• Less loss of strength
• No interference
• Greater bandwidth for more information per second
• Increased security