Skip to content

3.3.1 Progressive and stationary waves

3.3.1.1 Progressive waves

Mechanical waves

  • Involve particles in a substance vibrating

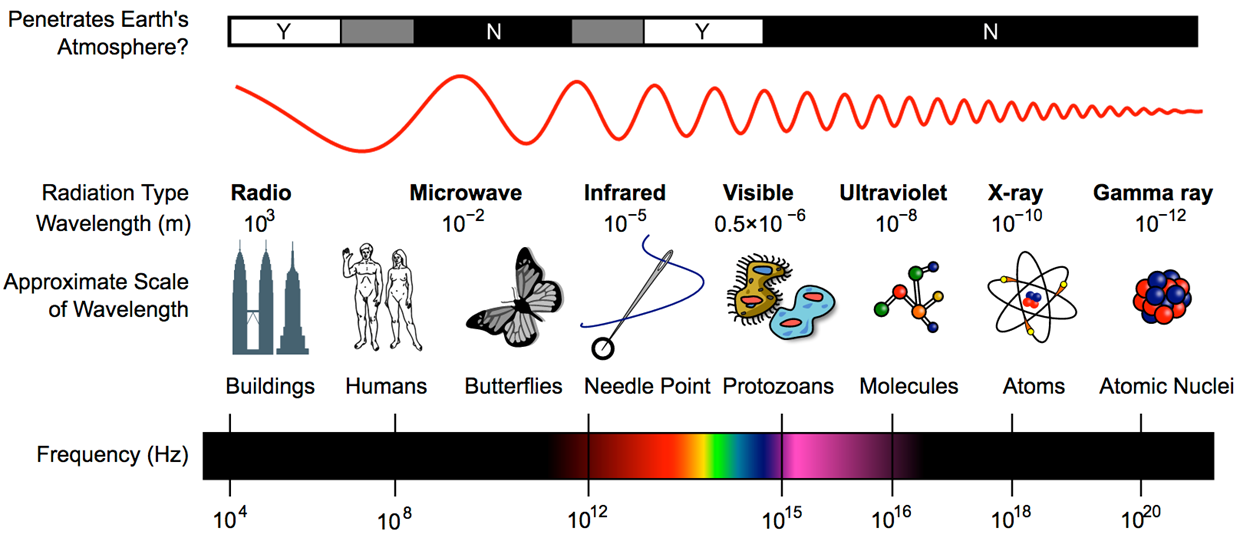
Electromagnetic waves

  • Travel through space without the need for a medium

Electromagnetic spectrum

  • Exported image|700x307

Progressive wave

  • A wave that transfers energy and momentum from one point to another without transferring the medium itself
  • Made up of particles of an oscillating medium

Terminologies

Term Definition
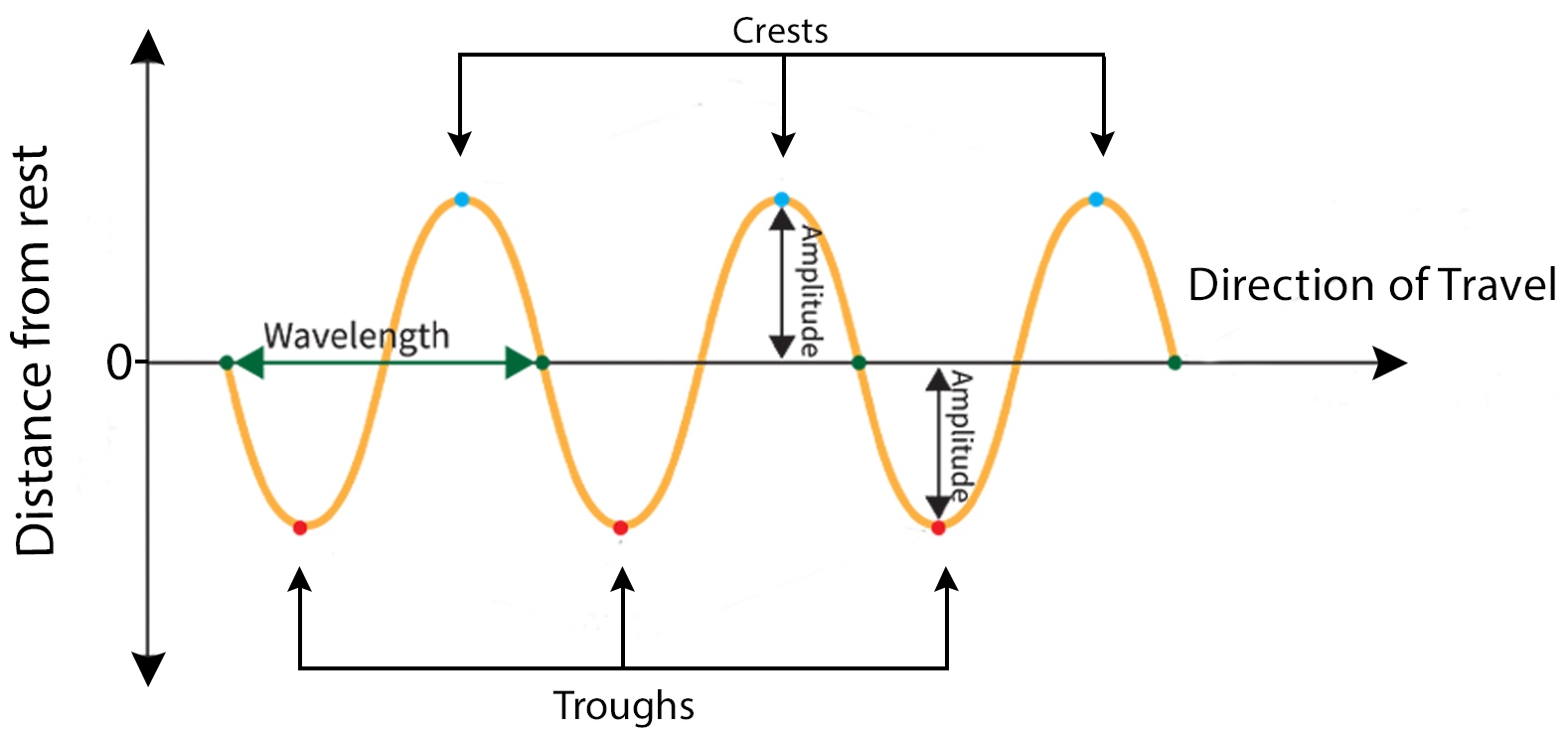
Displacement The vibrating particle's distance and direction from its equilibrium position
Amplitude A wave's maximum displacement from the equilibrium position (unit = m)
Frequency The number of complete oscillations passing through a point per second (unit = Hz)
Period The time taken to make one oscillation (unit = s)
Wavelength The length of one whole oscillation (e.g. the distance between successive peaks/troughs) (unit = m)
Speed Distance travelled by the wave per unit time (unit = \(ms^{-1}\))
Phase The fraction of a cycle a vibrating particle has completed since the start of the cycle
Cycle One complete cycle of a wave is from maximum displacement to next maximum displacement
  • Exported image|612x286

Phase difference

  • The fraction of a cycle between the vibration of two particles
  • \(\text{phase difference in radians} = \frac{2 \pi d}{\lambda} = \frac{2 \pi \times \text{distance between two points}}{\text{wavelength}}\)

In phase

  • Two points on a wave are in phase if they are both at the same point of the wave cycle
  • Same displacement and velocity
  • Phase difference is a multiple of 360° / \(2\pi\)

Completely out of phase / in anti-phase

  • \((2n + 1)\pi\) apart in phase

Wave speed

  • \(c = f\lambda\)

Frequency / period conversion

  • \(f = \frac{1}{T}\)
  • \(T = \frac{1}{f}\)

Properties of waves

  • Reflection
  • Refraction
  • Diffraction

3.3.1.2 Longitudinal and transverse waves

Longitudinal and transverse waves

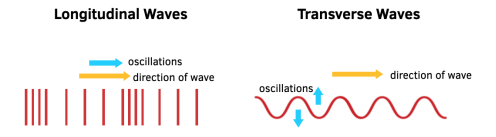
  • Transverse waves
    • The particles oscillate perpendicular to the direction of travel of the wave
    • Can be polarised
    • e.g. EM waves, waves on a string
  • Longitudinal waves
    • The particles oscillate parallel to the direction of travel of wave
    • The particles get compressed so they have more energy than the particles around them
    • When they vibrate they transfer energy to particles nearby \(\rightarrow\) more compressions
    • Cannot be polarised
    • Cannot travel in vacuums (require a medium to propagate)
    • e.g. sound waves
  • Exported image|571x158

Types of waves

  • Mechanical waves
    • Oscillations of the particles of the medium
  • Electromagnetic waves
    • Oscillating electric and magnetic field that progress through space without the need for a substance
    • Transverse waves
    • All have the same speed in vacuum (\(3 \times 10^8 \text{ ms}^{-1}\))

Polarisation

  • Can only happen for transverse waves
    • Oscillations of particles / fields are perpendicular to the direction of energy propagation
    • Wave's oscillations exist in more than one plane initially
  • Particle oscillations restricted to a single plane perpendicular to the direction of wave propagation
  • Cannot occur on longitudinal waves as it does not oscillate perpendicular to the direction of travel
  • (Transverse waves are called plane-polarised if the vibrations occur in one plane only, more than one plane = unpolarised)

Polarising filter

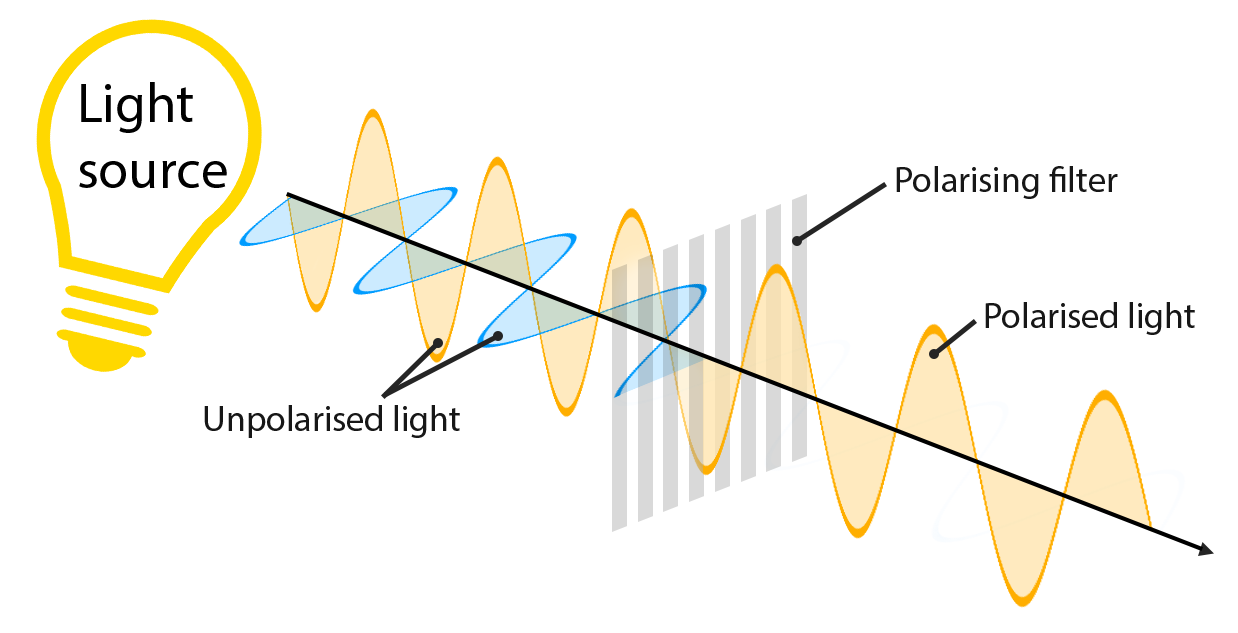
  • Linear polarized 3D glasses and the physical shape...|500x256
  • Only the wave oscillating along the transmission axis can completely pass through
  • Greater angle between wave + axis = lower light intensity
  • Waves oscillating perpendicular to the transmission axis cannot pass through = 0 intensity

Why only transverse waves can be polarised

  • Transverse waves oscillate perpendicular to direction of travel of wave
    • They initially oscillate in many different planes
    • Intensity is reduced due to oscillations being limited to one plane only
  • Longitudinal waves oscillate parallel to direction of travel of wave
    • There is no perpendicular plane to restrict the oscillations to

Applications of polarisation

  • Polaroid sunglasses
    • Vertical transmission axis
    • Reduce glare by blocking (nearly all) horizontally polarised light reflected from water and glass
    • Only oscillations in the plane of the filter is allowed, other directions absorbed
    • Only transmits the vertical component of the unpolarised light from objects
      • 50% of the original light passes through
    • Reduces light from surface reflection more than light from objects so it is easier to see
  • EV and radio signals
    • Plane-polarised by the orientation of the rods on the transmitting aerial
    • The receiving aerial must be aligned in the same plane of polarisation to receive the signal at full strength

3.3.1.3 Principle of superposition of waves and formation of stationary waves

The principle of superposition

  • When two or more waves arrive at one point, the resultant displacement is the sum of the displacement of each wave

Constructive interference

  • Occurs when 2 waves have displacement in the same direction (arrives in phase)

Destructive interference

  • Occurs when one wave has positive displacement and the other has negative displacement (arrives out of phase)
  • If the waves have equal but opposite displacements (\(\pi\) rad out of phase), total destructive interference occurs (zero amplitude)

Stationary waves

  • Waves where there is no net transfer of energy and momentum from one point to another
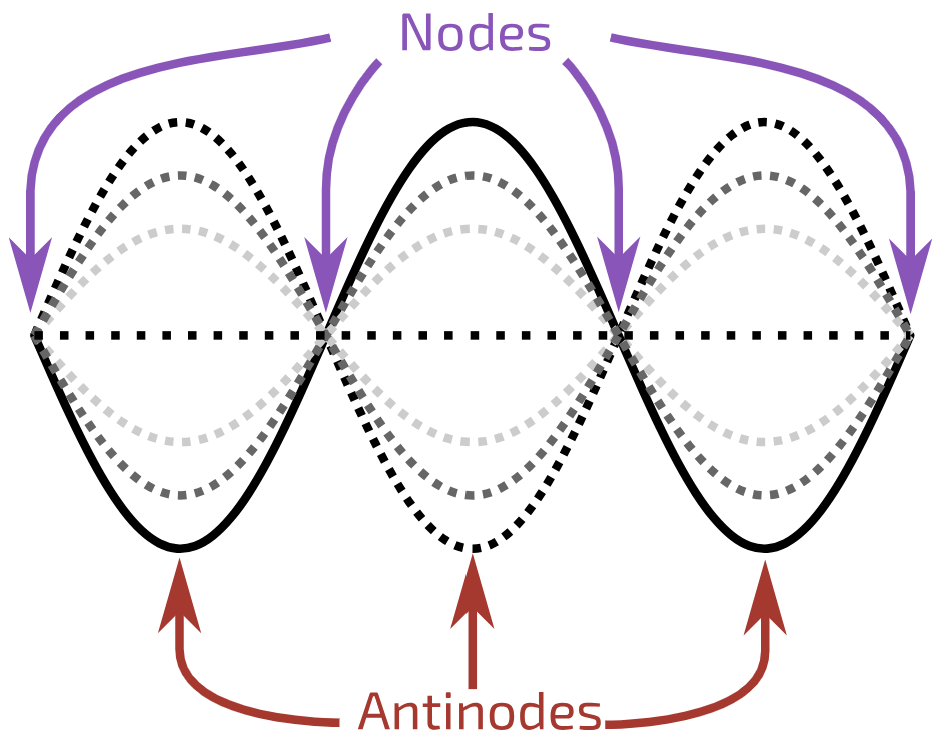
  • Exported image|307x241

Formation of stationary waves

  • Formed by the superposition of two or more progressive waves of the same frequency and wavelength and similar amplitudes passing through each other in opposite directions in the same medium
    • (The waves are emitted by ..., reflected through 180° by ...)
  • Amplitudes of the two waves do not need to be the same
  • Constructive interference occurs at where the waves meet in phase so antinodes are formed
  • Destructive interference occurs at where the waves meet completely out of phase so nodes are formed

Nodes

  • Fixed points in a stationary wave where the amplitude is minimum (usually zero)
  • Distance between 2 nodes = \(\frac{\text{wavelength}}{2}\)

Antinode

  • Fixed point in a stationary wave pattern where the amplitude is maximum
  • The particles have maximum energy at the antinode

Progressive waves + stationary waves comparison

Stationary Progressive
Energy & momentum No net transfer of energy from one point to another through space Energy and momentum is transferred from 1 point to another
Wavelength Wavelength = 2 \(\times\) distance between adjacent nodes Wavelength = distance between 2 particles at the same phase
Frequency All particles except the particles at the nodes vibrate at the same frequency All particles vibrate at the same frequency
Amplitude The amplitude varies from minimum (0) at the nodes to maximum at the antinode The amplitude is the same for each point along wave
Phase difference between 2 particles (rad) Particles immediately on either side of a node are moving in opposite directions (180° out of phase)
Between adjacent nodes all particles are vibrate in phase
\(\text{phase difference} = m\pi = \text{number of nodes between 2 particles} \times \pi\)		 \(\text{phase difference} = \frac{2 \pi d}{\lambda}\)
Adjacent points vibrate with different phase

Examples of stationary waves

  • Transverse stationary waves
    • String fixed at one end and the other end is fixed to a driving oscillator / plucked
      • Wave reflected at the fixed end of the string by 180°
      • Two waves superpose with each other
      • Both ends are fixed so both ends of the string are always nodes
    • Stationary microwaves
      • Reflected on a soft surface
      • The reflected end is an antinode, the emitter end is a node
      • A microwave probe can be used to find the nodes and antinodes
  • Longitudinal stationary waves
    • Sound waves
      • Speaker causes the wave \(\rightarrow\) antinode
      • Open end: when air leaves the tube the pressure around it is lower so it expands \(\rightarrow\) air pushed back to the tube \(\rightarrow\) antinode
      • Close end: reflects the wave which reverses its displacement \(\rightarrow\) cancelled out by upcoming wave \(\rightarrow\) node

Harmonics

  • The number of antinodes on the string

First harmonic frequency / fundamental frequency

  • The lowest frequency at which a stationary wave forms
  • Forms a stationary wave with two nodes and a single antinode
  • Distance between adjacent nodes = half a wavelength
  • \(\lambda = 2L\)
  • \(f_{0} = \frac{c}{2L} = \frac{1}{2L} \sqrt{\frac{T}{\mu}}\) (\(T = \text{tension in the wire}, \mu = \frac{m}{L} = \text{mass per unit length}\))
  • \(\text{nth harmonic frequency} = n \times \text{first harmonic frequency} = nf_{1}\)
  • nth harmonic frequency = nodes at a distance of \(\frac{L}{n}\)

Factors affecting the fundamental frequency

  • Mass per unit length
  • Tension
  • Length
  • Temperature

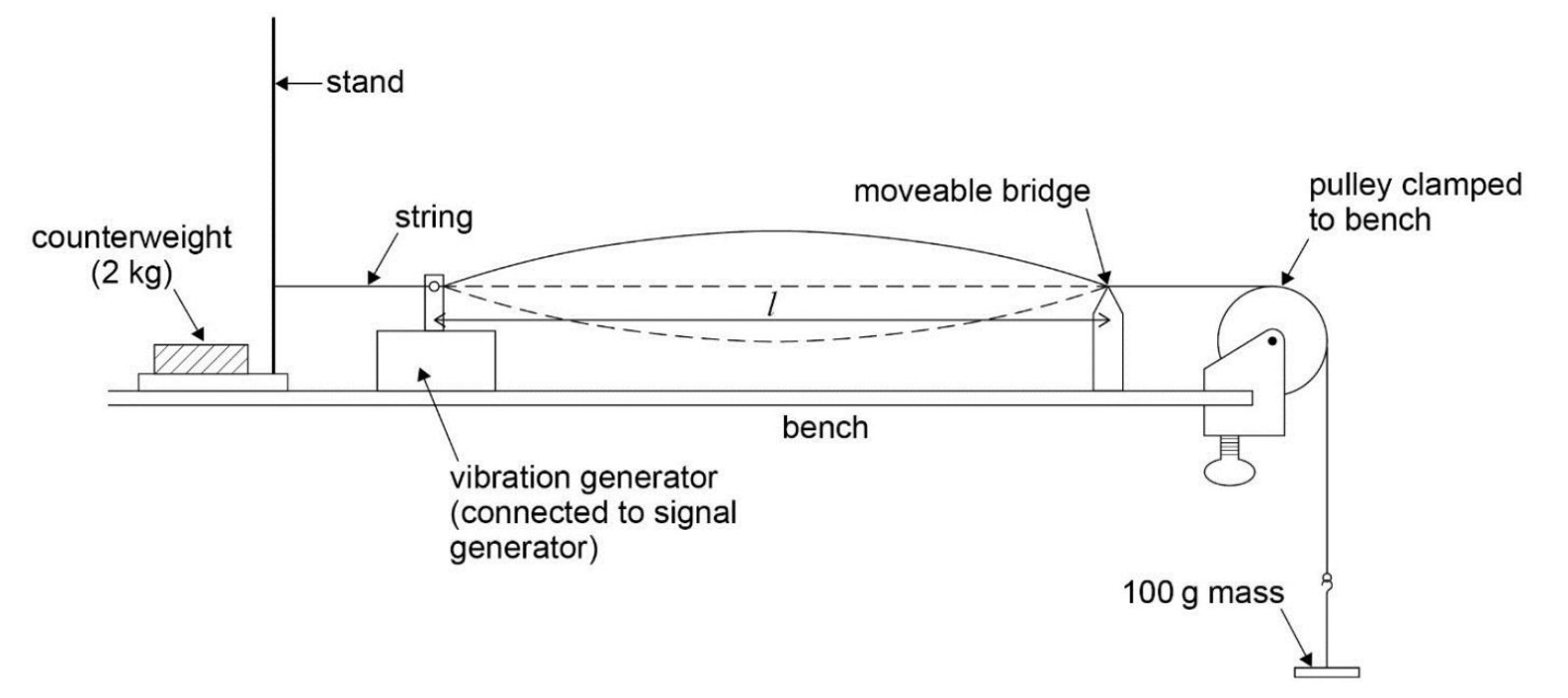
Required Practical 1 - Stationary Waves

Frequency vs length / tension / mass per unit length

  • Keep other variables constant
  • Use a signal generator + vibrator connected to signal generator to produce the vibrations
  • Measure length using ruler / tension by hanging mass at one end / mass per unit length by changing the wire
  • Graph of \(f\) vs. \(\frac{1}{l}\) / \(f\) vs \(\sqrt{T}\) / \(f\) vs \(\frac{1}{\sqrt{\mu}}\)
  • Exported image|652x290