3.2.2 Electromagmetic radiation and quantum phenomena

3.2.2.1 The photoelectric effect

The photoelectric effect

Photoelectrons are emitted from the surface of a metal after light above a certain frequency (threshold frequency) is shone on it

Work function (\(\phi\))

The minimum energy to remove an electron from the metal surface when the metal is at zero potential

Stopping potential (\(V_{s}\))

The PD needed to apply across the metal to stop the photoelectrons with the maximum KE (\(E_{k(max)}\))
Minimum energy needed per unit charge to stop photoelectric emissions
\(E_{k(max)} = e \times V_{s}\)

Threshold frequency

The minimum frequency of the radiation / light / photon needed to liberate an electron from the surface of a material
\(hf > \phi\)
\(f_{min} = \frac{\phi}{h}\)

Why wave theory doesn't work

There is no photoemission below the threshold frequency even with bright light
- Wave theory would allow gradual accumulation of energy to cause emission
- Any frequency of light should be able to cause electron emission
Electrons are emitted with no noticeable decay
- In wave theory time would elapse while an electron gains sufficient energy to leave the surface
Intensity of the light does not affect the KE of the emitted electrons
- High intensity waves would be expected to give higher KE to an electron

Explanation with the photon model

When light is incident on a metal surface an electron at the surface absorbs a single photon from the incident light and gains energy equal to \(hf\)
An electron can leave the metal surface if the energy gained > the work function of the metal
Excess energy gained becomes KE of the photoelectron

Effect of increasing the intensity of light

There are more photons striking the surface per second
Current increases as the number of electrons emitted per second increases

Photoelectric equation

\(E = hf = \phi + E_{k(max)}\)
\(E_{k(max)} = hf - \phi\)
Graph
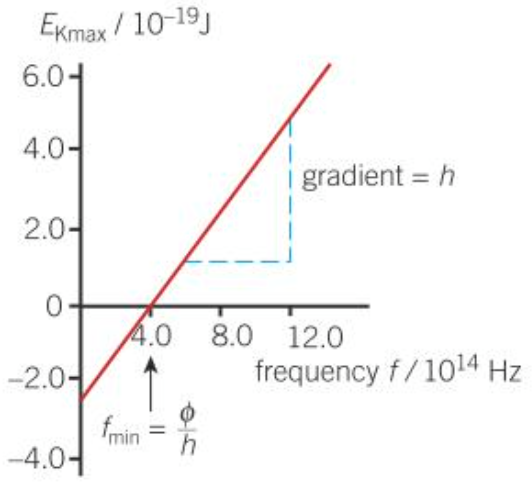
- Gradient = \(h\)
- y-intercept = \(-\phi\)

Energy level of emitted electrons

There exists a maximum value of energy
Energy of photons are constant (\(hf\))
One to one interaction between photon and electron so a fixed amount of KE is transferred
The energy required to remove an electron varies so the KE of electrons varies
- Max KE = photon energy - work function
- Deeper electrons require more energy to remove than surface electrons

3.2.2.2 Collisions of electrons with atoms

Electron energy level

Electrons in atoms can only exist in discrete energy levels
These electrons can gain energy from collisions with free electrons / absorbing photons

Excitation

Electrons move up in energy level
It will quickly return to its original energy level (the ground state) and release energy gained as photons

Ionisation

Electrons gain enough energy to be removed from the atom entirely
Occurs if the energy of the free electron is greater than the ionisation energy

Excitation energies

The energy values at which an atom absorbs energy

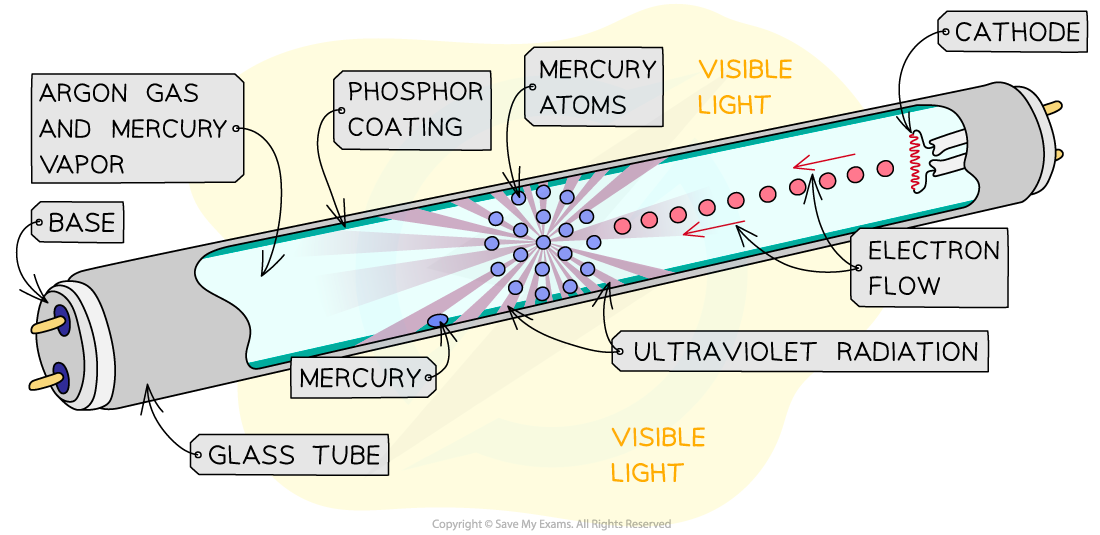
Fluorescent tube

Filled with mercury vapour
High voltage applied which accelerates free electrons through the tube
Free electrons collide with the mercury atoms
Electrons in the mercury atoms are raised to a higher energy level
The mercury atom become ionised \(\rightarrow\) release more free electrons
The new free electrons collide with the mercury atoms, causing them to become excited
Mercury atoms de-excites and relaxes to a lower energy level
- They release photons of energy equal to the energy difference between the levels
- Frequency is mostly in the UV range
The fluorescent coating on the inside of the tube absorbs these UV photons and therefore electrons in the atoms of the coating become excited and de-excite releasing photons of visible light
Emitted radiation consists of (a range of) lower photon energies / frequencies or longer wavelengths

Why electrons only need a minimum energy level to excite an atom

An exact amount of energy is needed to excite an atom to a certain energy level
All of the photon's energy will be absorbed in a 1 to 1 interaction
Electron can transfer part of its energy to cause the excitation and continue moving at a lower KE

3.2.2.3 Energy levels and photon emission

Ground state

When electrons / atoms are in there lowest energy state / most stable state

Excited state

Electron (in ground state) has moved to higher energy level / shell

Ionisation energy

The minimum energy to remove an electron from an atom from the ground state

De-excitation

The electron configuration in an excited atom is unstable due to a vacancy in the shell that the excited electron left
The vacancy is filled by an electron from an outer shell transferring to it

Possible energy level of atoms

An atom can only have certain levels of energy
Each allowed energy level = a certain electron configuration of the atom

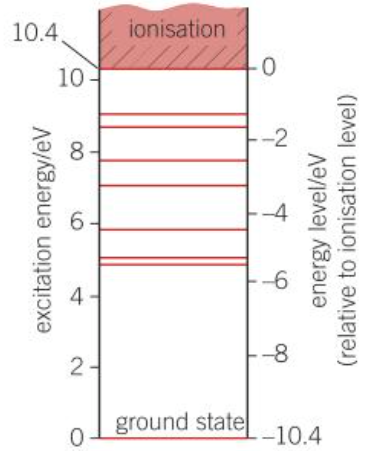
Line spectrum

Obtained by passing the light from a fluorescent tube through a diffraction grating or prism
Each line = a specific wavelength of light emitted by the tube = corresponds a specific photon energy emitted
Show that electrons in atoms can only transition between discrete energy levels

Line absorption spectrum

Continuous spectrum with black lines at certain intervals
Obtained by passing white light through a cooled gas
Black lines represent the possible differences in energy levels
- The atoms in the gas can only absorb photons of an energy equal to the exact difference between two energy levels

Why only certain frequencies of light can be absorbed

Electrons occupy discrete energy levels
They need to absorb an exact amount of energy to move to a higher level
Photons need to have certain frequency to provide this energy (\(E=hf\))
Energy required is the same for a particular atom
All energy of the photon is absorbed in 1 to 1 interaction between photon + electron

Energy level difference

Difference between two energy levels = a line in the line spectrum = a specific photon energy emitted by a fluorescent tube / absorbed in a line absorption spectrum
Energy of photon emitted = energy lost by the electron = energy lost by the atom
Energy of the emitted photon \(hf = E_{1} - E_{2}\)

3.2.2.4 Wave-particle duality

Evidence for wave-particle duality of light / EM waves

Acting as wave: diffraction and interference
Acting as particle: photoelectric effect

De Broglie hypothesis

Matter particles have a dual wave-particle nature

Evidence for de Broglie hypothesis

Collisions by incident electrons move electrons in atoms between energy levels
Photon emitted when atoms de-excite or electrons move to lower energy levels
Wave properties of electrons
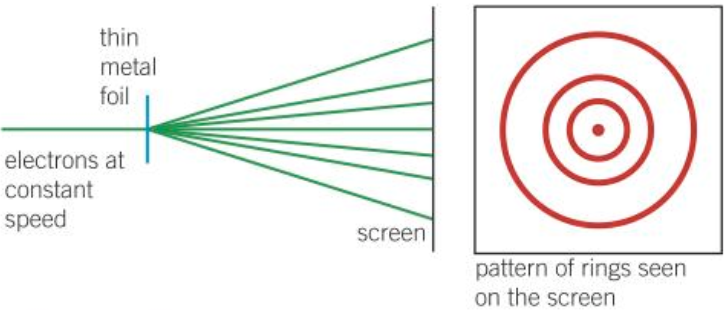
- Diffraction of electrons by a metal crystal
- Electrons can be diffracted, shown as concentric rings on screen
- Foil / graphite causes electrons to travel in particular directions
- Bright rings / maximum intensity occurs where waves arrive in phase and interfere constructively
- Particle behaviour would only produce a circle of light as particles scatter randomly
- Only waves can experience diffraction \(\rightarrow\) electrons also have a dual wave-particle nature
- Similar to diffracting grating maxima when \(n \lambda = d \sin \theta\)
Particle properties of electrons
- Electrons must provide enough kinetic energy for light to be emitted
- Instant light as electron can provide the energy in discrete amounts to excite the atoms
- Waves \(\rightarrow\) energy will accumulate gradually so time is needed until light is emitted & light will always be emitted no matter how low the energy is
Property later also shown for other particles

De Broglie wavelength

The wavelength of the wave-like behaviour of a matter particle
\(\lambda = \frac{h}{p} = \frac{h}{mv}\)
Higher particle momentum = shorter wavelength = less diffraction = concentric rings of the interference pattern become closer

Change in understanding of matter

Knowledge and understanding of the nature of matter changes over time in line with new experimental evidence gathered
Such changes need to be evaluated through peer review and validated by the scientific community before being accepted