5.1.3 Acids, bases and buffers
Definitions
| Term | Definition |
|---|---|
| Monobasic acid | 1 hydrogen ion can be replaced per molecule in acid-base reaction |
| Dibasic acid | 2 hydrogen ions can be replaced per molecule in acid-base |
| Tribasic acid | 3 hydrogen ions can be replaced per molecule in acid-base reaction |
| End point | Where the indicator changes colour |
Brønsted–Lowry acids and bases
Brønsted-Lowry acids and bases
- Brønsted-Lowry acid = a proton donor
- Brønsted-Lowry base = a proton acceptor
Conjugate acid-base pairs
- Two species that can be interconverted by transfer of a proton (cannot be more than 1 protons)
- \(\text{Conjugate acid (aq)} \rightleftharpoons H^+(aq) + \text{Conjugate base (aq)}\)
pH and [H+(aq)]
pH formula
- \(pH = -\log [H^+]\)
- \([H^+] = 10^{-pH}\)
Acid dissociation constant \(K_a\)
- For reaction \(HA(aq) \rightleftharpoons H^+(aq) + A^-(aq)\)
- \(K_a = \frac{[H^+(aq)][A^-(aq)]}{[HA(aq)]}\)
- Unit = \(mol \cdot dm^{-3}\)
- Changes with temperature, recorded values normally standardised at 25°C
\(pK_a\) values
- \(pK_a = -\log K_a\)
- \(K_a = 10^{-pK_a}\)
- Used when \(K_a\) is small
- Stronger acid = higher \(K_a\) + lower \(pK_a\)
pH calculations
- pH for strong monobasic acid
- Assume \([H^+(aq)] = [HA(aq)]\) (= acid concentration)
- pH for weak monobasic acid
- \(K_a \approx \frac{[H^+(aq)]^2}{[HA(aq)]}\)
- Precise formula: \(K_a = \frac{[H^+(aq)]_{eqm}[A^-(aq)]_{eqm}}{[HA(aq)]_{start} - [H^+(aq)]_{eqm}}\)
- Assumptions:
- Equal concentration of \(H^+\) and \(A^-\): \([H^+(aq)]_{eqm} \approx [A^-(aq)]_{eqm}\) (Not valid for very weak acids / very dilute solutions)
- Dissociation is negligible: \([HA(aq)]_{eqm} \approx [HA(aq)]_{start}\) (Not valid for stronger weak acids with \(K_a > 10^{-2} \ mol \cdot dm^{-3}\) / very dilute solutions)
Ionic product of water \(K_w\)
- How water ionises: \(H_2O(l) \rightleftharpoons H^+(aq) + OH^-(aq)\)
- \(K_w = [H^+(aq)][OH^-(aq)]\)
- \(K_w\) at 298K = \(1.00 \times 10^{-14} \ mol^2 \cdot dm^{-6}\) (varies with temperature, can assume it is this value unless stated otherwise)
Buffers: action, uses and calculations
Buffer solution
- A system that minimises pH changes on addition of small amounts of acid or alkali
- Contains a weak acid + its conjugate base in a salt
Preparing buffer solutions
- Mixing weak acid + one of its salts
- e.g. \(CH_3COOH + CH_3COONa\)
- Weak acid partially dissociates when added to water \(\rightarrow\) provide the weak acid component
- Salts of weak acids = ionic compounds \(\rightarrow\) completely dissolve + dissociate into ions in water \(\rightarrow\) provide the conjugate base
- Adding a strong alkali to an excess of a weak acid
- e.g. excess \(CH_3COOH + NaOH\)
- Weak acid partially neutralised by the alkali \(\rightarrow\) conjugate base formed
- Some weak acid left unreacted
- Result: mixture of salt of weak acid + unreacted weak acid
How buffer solutions work
- Equilibrium established e.g. \(HA(aq) \rightleftharpoons H^+(aq) + A^-(aq)\)
- Acid / \(H^+(aq)\) added
- \([H^+(aq)]\) increases
- \(H^+(aq)\) ions react with the conjugate base (\(A^-\))
- Equilibrium position shifts to the left
- Most of the \(H^+(aq)\) ions added is used up so pH change is minimised
- Alkali / \(OH^-(aq)\) added
- \([OH^-(aq)]\) increases
- \(OH^-(aq)\) reacts with \(H^+\) to form water so \(H^+\) is used up
- The equilibrium moves to RHS to replace most of the \(H^+\) used up and minimise the pH change
- HA dissociates \(\rightarrow\) shifts the equilibrium to the right \(\rightarrow\) restore most of the \(H^+(aq)\) ions
- Overall reaction: \(HA(aq) + OH^-(aq) \rightarrow H_2O(l) + A^-(aq)\)
Calculating pH of a buffer solution
- Acid + alkali: calculate how much \(A^-\) is in the solution and how much \(HA\) is left
- Acid + salt: assume all \(A^-\) from salt
- Assume \([HA]\) stays constant in both cases
- \([H^+(aq)] = K_a \times \frac{[HA(aq)]}{[A^-(aq)]}\)
- Quick formula: \(pH = pK_a + \log \frac{[\text{salt}]}{[\text{acid}]}\)
Control of blood pH
- Blood plasma needs to have a pH between 7.35 to 7.45
- pH below 7.35 \(\rightarrow\) acidosis (fatigue, shortness breath, shock, death)
- pH above 7.45 \(\rightarrow\) alkalosis (muscle spasms, light headedness, nausea)
- pH maintained by carbonic acid (\(H_2CO_3\)) - hydrogencarbonate (\(HCO_3^-\)) buffer system: \(H_2CO_3 \rightleftharpoons H^+ + HCO_3^-\)
Neutralisation
pH titration curve
- Weak base - steeper gradient for basic section
- Weak acid - steeper gradient for acidic section
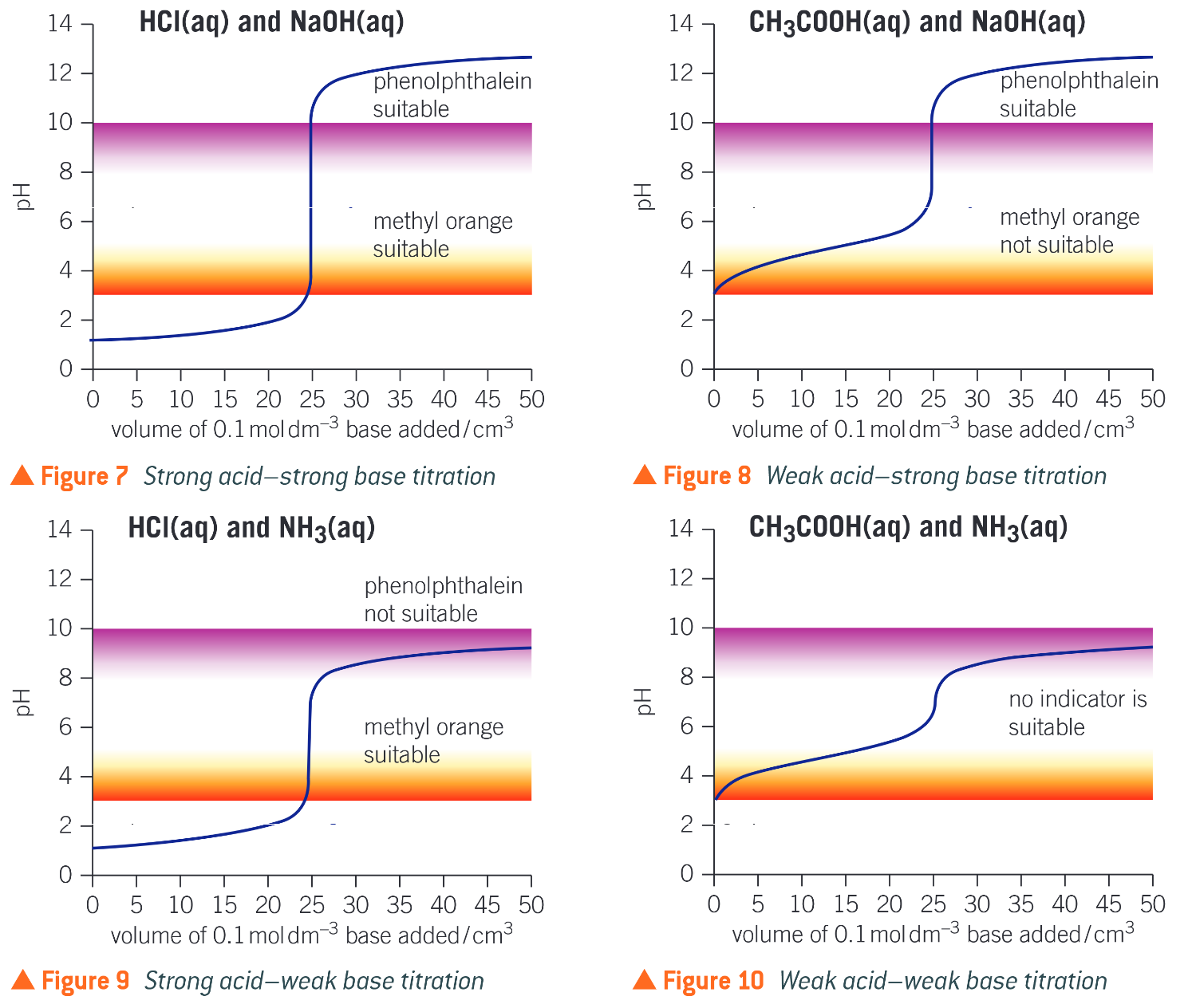
- (Acid to base: mirror the shapes)
Equivalence point
- Halfway up the vertical section
- Where the amount of acid exactly neutralises the amount of alkali
Indicator colour change explanation
- Indicator = weak acid with distinctively different colour to conjugate base
- \(HIn(aq) \rightleftharpoons H^+(aq) + In^-(aq)\)
- Equilibrium position shifts toward LHS in acidic conditions
- Equilibrium position shifts toward RHS in basic conditions
Common indicators

- (Most indicators change colour over a range of 2 pH units)
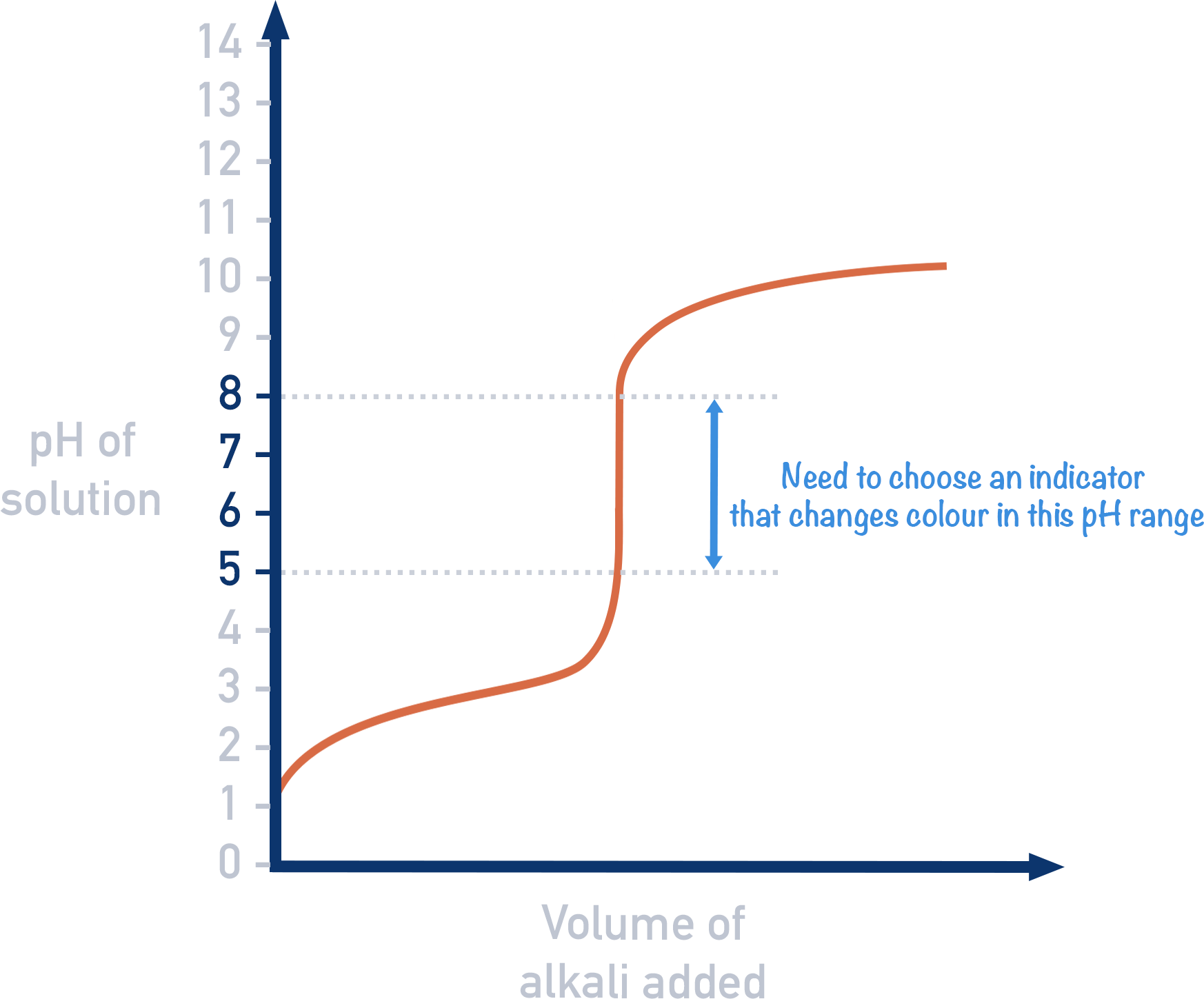
Choice of suitable indicators for titration
- Choose indicator with a colour change range that coincides with the vertical section of the pH titration curve
- Ideally same end point and equivalence point
- End point not in vertical section: range of volumes for colour change is too big
- No indicator suitable for weak acid-weak base titrations as there is no vertical section + even at steepest requires several \(cm^3\) to pass through a range of 2 pH units