3.2.1 Enthalpy changes

Definitions

Term	Definition
Enthalpy	Measure of heat energy in a chemical system
Chemical system	The atoms, molecules or ions making up the chemicals
Activation energy / \(E_{a}\)	The minimum energy required for a reaction to take place
Standard state	The physical state of a substance under standard conditions
Enthalpy change of reaction / \(\Delta_{r} H\)	The enthalpy change associated with a stated equation in the molar quantities shown in the equation
Enthalpy change of formation / \(\Delta_{f} H\)	The enthalpy change that takes place when 1 mole of a compound is formed from its elements
Enthalpy change of combustion / \(\Delta_{c} H\)	The enthalpy change that takes place when 1 mole of a substance reacts completely with oxygen
Enthalpy change of neutralisation / \(\Delta_{neut} H\)	The enthalpy change that accompanies the reaction of an acid by a base to form 1 mole of \(H_2O(l)\)
Enthalpy change of solution / dissolution	The enthalpy change when 1 mole of a substance is completely dissolved in water
Hess's Law	The enthalpy change in a chemical reaction is independent of the route it takes

(standard ... = under standard conditions : 298 K & 100 kPa, with all reactants and products in their standard states)

Enthalpy changes

Enthalpy change

• \(\Delta H = H(products) - H(reactants)\)
• Can be positive (endothermic) or negative (exothermic)

Types of reactions

• Exothermic reaction: Energy transferred from the system to the surroundings
• Endothermic reaction: Energy transferred from the surroundings to the system

Enthalpy profile diagrams

Exothermic	Endothermic
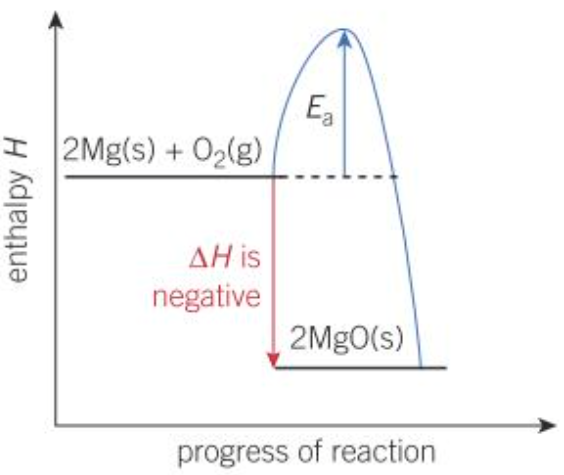\(\Delta H\) is negative	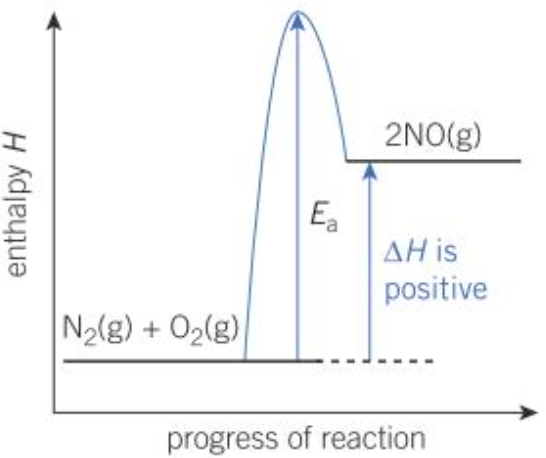\(\Delta H\) is positive

• The activation energy can normally be omitted when there are > 1 energy changes

Standard conditions

• Shown with symbol \(^\ominus\) / °
• Standard pressure = 100 kPa / \(1 \times 10^5\) N \(m^{-2}\) / 1 atm
• Standard temperature = 298 K / 25 °C
• Standard concentration = 1 mol \(dm^{-3}\) / 1 M
• Substances will be in their normal physical states (standard states)

Measuring energy changes

• Use the equation \(q = mc\Delta T\)
• Energy change for the system = \(-q\) (if heat lost to surroundings)

Determine enthalpy change of combustion

• Measure certain volume of water, pour water into beaker
• Record initial temperature of water using a thermometer
• Add fuel to spirit burner + weigh spirit burner and fuel together
• Place spirit burner under beaker + light the burner
• Stir water with thermometer
• Extinguish flame after about 3 mins
• Record the maximum temperature reached
• Re-weigh spirit burner
• Work out the mass of fuel burnt hence the amount of fuel burnt in moles
• Work out energy change with \(q = mc\Delta T\)
• \(\text{Enthalpy change of combustion} = -\frac{q}{n}\)

Reasons for inaccuracies

• Heat loss to surroundings \(\rightarrow\) less exothermic than expected
• Incomplete combustion of fuel (black layer soot on calorimeter) \(\rightarrow\) less exothermic than expected
• Non-standard conditions \(\rightarrow\) more or less exothermic than expected
• Evaporation of fuel
  • Less exothermic
  • Seems to have used more fuel than actual
  • Extinguish the spirit burner ASAP after the experiment + reweigh the spirit burner

Determine enthalpy change of reaction

• Carry out reaction in polystyrene cup with thermometer clamped so that it stands in it
• Surroundings = the reaction solution (may assume density and specific heat capacity are the same as water)
• 

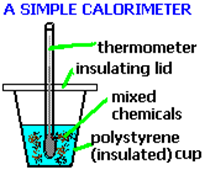
Determining the enthalpy change of neutralisation

• Make one reactant excess so the amount of water formed is fixed
• In theory all acid and alkali should release the same amount of energy but in reality it isn't due to the different strengths of acid / alkali species

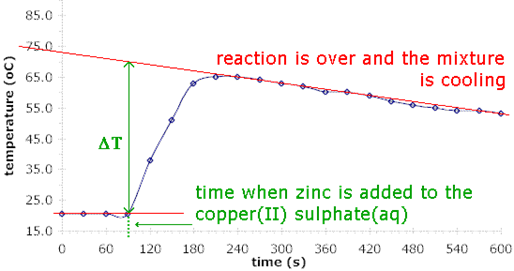
Cooling curve correction

• Add one reactant to the polystyrene cup
• Take temperature of the solution every 30s until temperature stays constant
• Add the other reactant + stir
• Measure temperature every 30s until temperature has fallen for several mins
• Plot a graph of temperature against time
• Extrapolate cooling curve section back to when second reactant added
• Find the theoretical \(\Delta T\) at that point of time
• 

Average bond enthalpy

• The enthalpy change when 1 mole of a bond is broken in the gas state
• Limitations: actual bond enthalpy can vary depending on the chemical environment of the bond

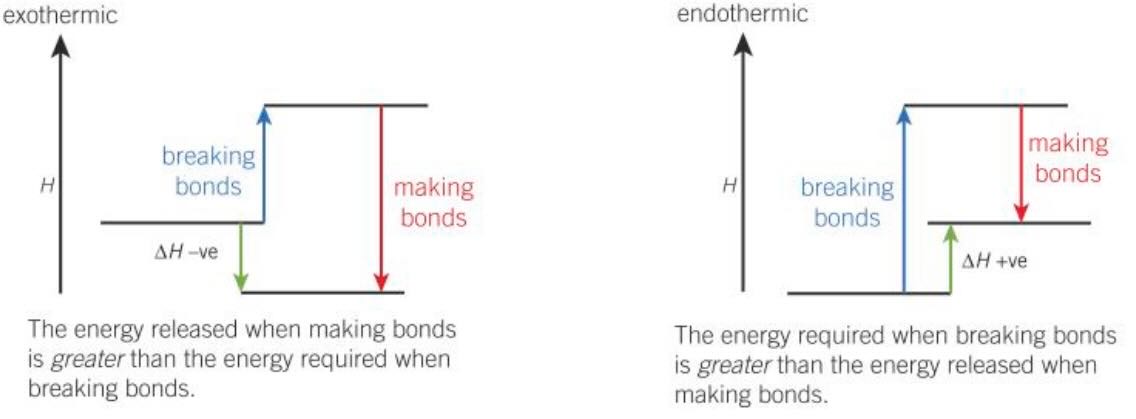
Endothermic / exothermic

• Endothermic
  • Bond breaking is endothermic
  • More energy required when breaking bonds than energy released when making bonds
  • \(\Delta H > 0\)
• Exothermic
  • Bond formation is exothermic
  • More energy released when making bonds than energy required when breaking bonds
  • \(\Delta H < 0\)
• 

Calculating enthalpy change from average bond enthalpies

• \(\Delta_{r} H = \Sigma (\text{bond enthalpies in reactants}) - \Sigma (\text{bond enthalpies in products})\)

Working out enthalpy change using Hess's Law

• Using enthalpy change of formation: \(\Delta_{r} H = \Sigma \Delta_{f} H (\text{products}) - \Sigma \Delta_{f} H (\text{reactants})\)
• Using enthalpy change of combustion: \(\Delta_{r} H = \Sigma \Delta_{c} H (\text{reactants}) - \Sigma \Delta_{c} H (\text{products})\)